Moving Object Segmentation in Point Cloud Data using Hidden Markov Models

Autonomous agents require the capability to identify dynamic objects in their environment for safe planning and navigation. Incomplete and erroneous dynamic detections jeopardize the agent's ability to accomplish its task. Dynamic detection is a challenging problem due to the numerous sources of uncertainty inherent in the problem's inputs and the wide variety of applications, which often lead to use-case-tailored solutions. We propose a robust learning-free approach to segment moving objects in point cloud data. The foundation of the approach lies in modelling each voxel using a hidden Markov model (HMM), and probabilistically integrating beliefs into a map using an HMM filter. The proposed approach is tested on benchmark datasets and consistently performs better than or as well as state-of-the-art methods with strong generalized performance across sensor characteristics and environments. The approach is open-sourced at https://github.com/vb44/HMM-MOS.

Probabilistic Height Grid Terrain Mapping for Mining Shovels using LiDAR

This paper explores the question of creating and maintaining terrain maps in environments where the terrain changes. The specific example explored is the construction of terrain maps from 3D LiDAR measurements on an electric rope shovel. The approach extends the height grid representation of terrain to include a Hidden Markov Model in each cell, enabling confidence-based mapping of constantly changing terrain. There are inherent difficulties in this problem, including semantic labelling of the LiDAR measurements associated with machinery and determining the pose of the sensor. Solutions to both of these problems are explored. The significance of this work lies in the need for accurate terrain mapping to support autonomous machine operation.

Concurrent Learning Based Tracking Control of Nonlinear Systems using Gaussian Process

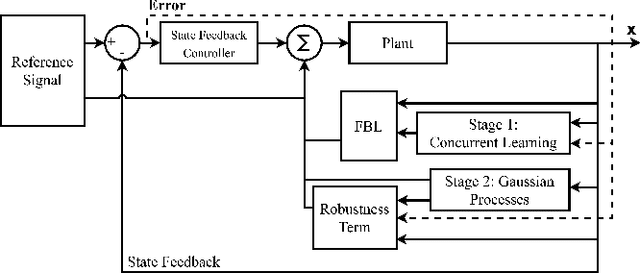
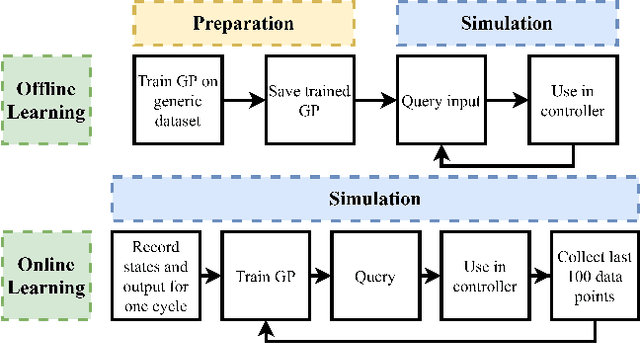
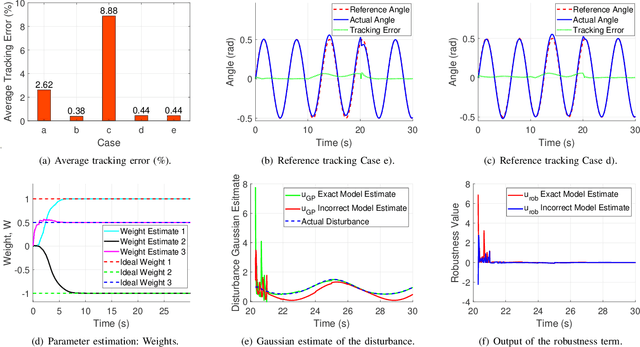
This paper demonstrates the applicability of the combination of concurrent learning as a tool for parameter estimation and non-parametric Gaussian Process for online disturbance learning. A control law is developed by using both techniques sequentially in the context of feedback linearization. The concurrent learning algorithm estimates the system parameters of structured uncertainty without requiring persistent excitation, which are used in the design of the feedback linearization law. Then, a non-parametric Gaussian Process learns unstructured uncertainty. The closed-loop system stability for the nth-order system is proven using the Lyapunov stability theorem. The simulation results show that the tracking error is minimized (i) when true values of model parameters have not been provided, (ii) in the presence of disturbances introduced once the parameters have converged to their true values and (iii) when system parameters have not converged to their true values in the presence of disturbances.