Vanessa Lopez Garcia
Neural Unification for Logic Reasoning over Natural Language
Sep 17, 2021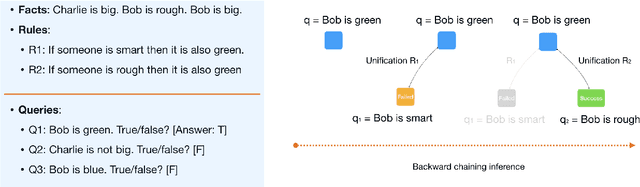
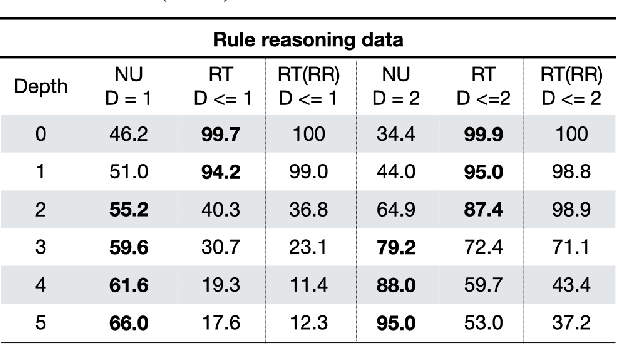
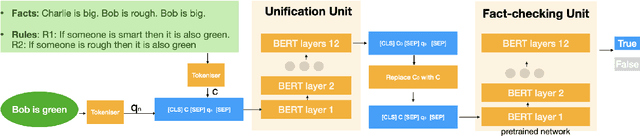

Abstract:Automated Theorem Proving (ATP) deals with the development of computer programs being able to show that some conjectures (queries) are a logical consequence of a set of axioms (facts and rules). There exists several successful ATPs where conjectures and axioms are formally provided (e.g. formalised as First Order Logic formulas). Recent approaches, such as (Clark et al., 2020), have proposed transformer-based architectures for deriving conjectures given axioms expressed in natural language (English). The conjecture is verified through a binary text classifier, where the transformers model is trained to predict the truth value of a conjecture given the axioms. The RuleTaker approach of (Clark et al., 2020) achieves appealing results both in terms of accuracy and in the ability to generalize, showing that when the model is trained with deep enough queries (at least 3 inference steps), the transformers are able to correctly answer the majority of queries (97.6%) that require up to 5 inference steps. In this work we propose a new architecture, namely the Neural Unifier, and a relative training procedure, which achieves state-of-the-art results in term of generalisation, showing that mimicking a well-known inference procedure, the backward chaining, it is possible to answer deep queries even when the model is trained only on shallow ones. The approach is demonstrated in experiments using a diverse set of benchmark data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge