Improving Article Classification with Edge-Heterogeneous Graph Neural Networks

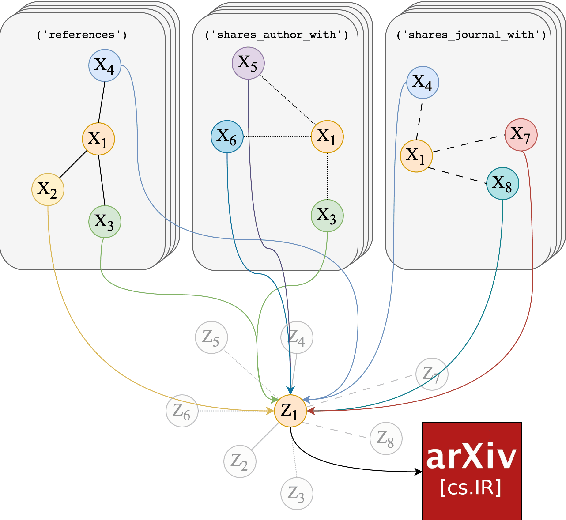
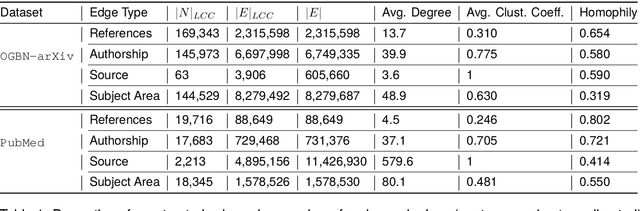
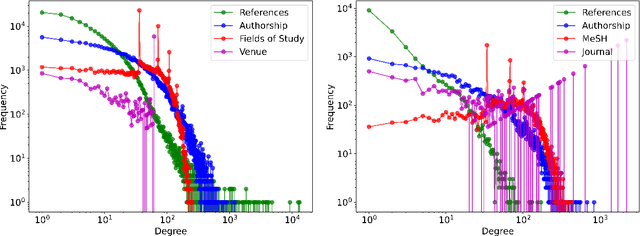
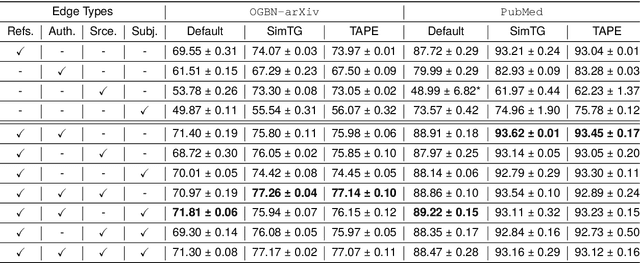
Classifying research output into context-specific label taxonomies is a challenging and relevant downstream task, given the volume of existing and newly published articles. We propose a method to enhance the performance of article classification by enriching simple Graph Neural Networks (GNN) pipelines with edge-heterogeneous graph representations. SciBERT is used for node feature generation to capture higher-order semantics within the articles' textual metadata. Fully supervised transductive node classification experiments are conducted on the Open Graph Benchmark (OGB) ogbn-arxiv dataset and the PubMed diabetes dataset, augmented with additional metadata from Microsoft Academic Graph (MAG) and PubMed Central, respectively. The results demonstrate that edge-heterogeneous graphs consistently improve the performance of all GNN models compared to the edge-homogeneous graphs. The transformed data enable simple and shallow GNN pipelines to achieve results on par with more complex architectures. On ogbn-arxiv, we achieve a top-15 result in the OGB competition with a 2-layer GCN (accuracy 74.61%), being the highest-scoring solution with sub-1 million parameters. On PubMed, we closely trail SOTA GNN architectures using a 2-layer GraphSAGE by including additional co-authorship edges in the graph (accuracy 89.88%). The implementation is available at: $\href{https://github.com/lyvykhang/edgehetero-nodeproppred}{\text{https://github.com/lyvykhang/edgehetero-nodeproppred}}$.

Data-driven reduced-order modelling for blood flow simulations with geometry-informed snapshots

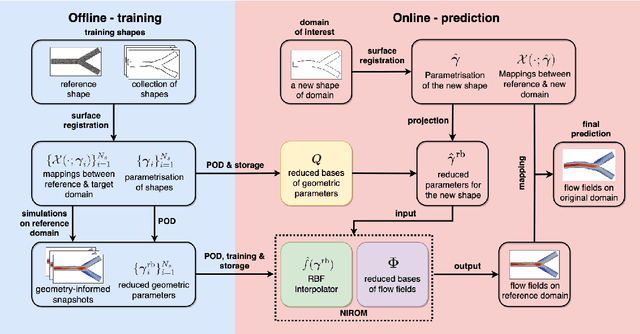
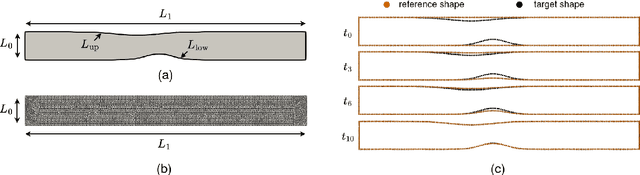
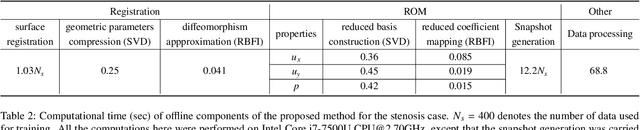
Computational fluid dynamics is a common tool in cardiovascular science and engineering to simulate, predict and study hemodynamics in arteries. However, owing to the complexity and scale of cardiovascular flow problems, the evaluation of the model could be computationally expensive, especially in those cases where a large number of evaluations are required, such as uncertainty quantification and design optimisation. In such scenarios, the model may have to be repeatedly evaluated due to the changes or distinctions of simulation domains. In this work, a data-driven surrogate model is proposed for the efficient prediction of blood flow simulations on similar but distinct domains. The proposed surrogate model leverages surface registration to parameterise those similar but distinct shapes and formulate corresponding hemodynamics information into geometry-informed snapshots by the diffeomorphism constructed between the reference domain and target domain. A non-intrusive reduced-order model for geometrical parameters is subsequently constructed using proper orthogonal decomposition, and a radial basis function interpolator is trained for predicting the reduced coefficients of the reduced-order model based on reduced coefficients of geometrical parameters of the shape. Two examples of blood flowing through a stenosis and a bifurcation are presented and analysed. The proposed surrogate model demonstrates its accuracy and efficiency in hemodynamics prediction and shows its potential application toward real-time simulation or uncertainty quantification for complex patient-specific scenarios.

Uncertainty quantification of a 3D In-Stent Restenosis model with surrogate modelling

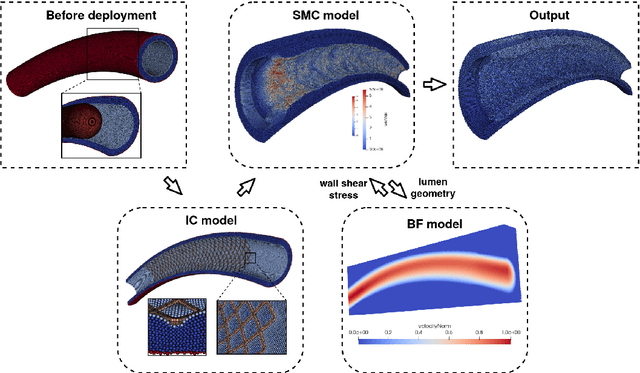
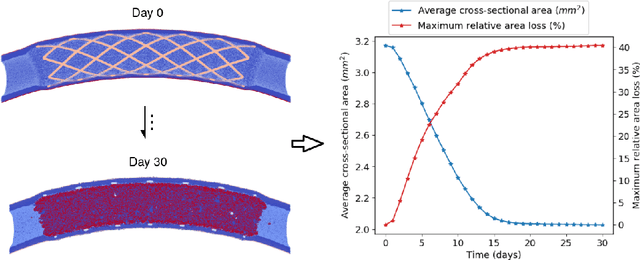
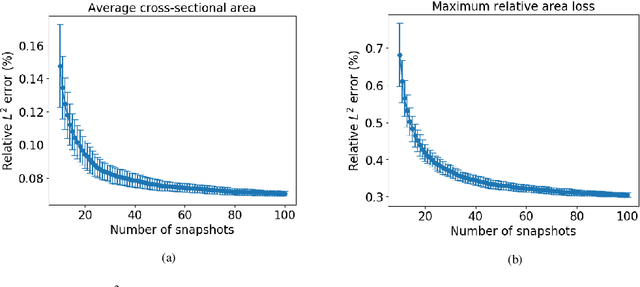
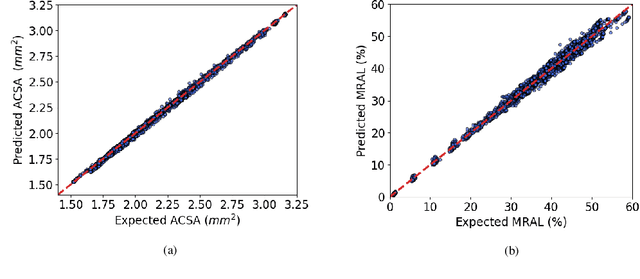
In-Stent Restenosis is a recurrence of coronary artery narrowing due to vascular injury caused by balloon dilation and stent placement. It may lead to the relapse of angina symptoms or to an acute coronary syndrome. An uncertainty quantification of a model for In-Stent Restenosis with four uncertain parameters (endothelium regeneration time, the threshold strain for smooth muscle cells bond breaking, blood flow velocity and the percentage of fenestration in the internal elastic lamina) is presented. Two quantities of interest were studied, namely the average cross-sectional area and the maximum relative area loss in a vessel. Due to the computational intensity of the model and the number of evaluations required in the uncertainty quantification, a surrogate model, based on Gaussian process regression with proper orthogonal decomposition, was developed which subsequently replaced the original In-Stent Restenosis model in the uncertainty quantification. A detailed analysis of the uncertainty propagation and sensitivity analysis is presented. Around 11% and 16% of uncertainty are observed on the average cross-sectional area and maximum relative area loss respectively, and the uncertainty estimates show that a higher fenestration mainly determines uncertainty in the neointimal growth at the initial stage of the process. On the other hand, the uncertainty in blood flow velocity and endothelium regeneration time mainly determine the uncertainty in the quantities of interest at the later, clinically relevant stages of the restenosis process. The uncertainty in the threshold strain is relatively small compared to the other uncertain parameters.