Integrating Fuzzy Logic with Causal Inference: Enhancing the Pearl and Neyman-Rubin Methodologies

In this paper, we generalize the Pearl and Neyman-Rubin methodologies in causal inference by introducing a generalized approach that incorporates fuzzy logic. Indeed, we introduce a fuzzy causal inference approach that consider both the vagueness and imprecision inherent in data, as well as the subjective human perspective characterized by fuzzy terms such as 'high', 'medium', and 'low'. To do so, we introduce two fuzzy causal effect formulas: the Fuzzy Average Treatment Effect (FATE) and the Generalized Fuzzy Average Treatment Effect (GFATE), together with their normalized versions: NFATE and NGFATE. When dealing with a binary treatment variable, our fuzzy causal effect formulas coincide with classical Average Treatment Effect (ATE) formula, that is a well-established and popular metric in causal inference. In FATE, all values of the treatment variable are considered equally important. In contrast, GFATE takes into account the rarity and frequency of these values. We show that for linear Structural Equation Models (SEMs), the normalized versions of our formulas, NFATE and NGFATE, are equivalent to ATE. Further, we provide identifiability criteria for these formulas and show their stability with respect to minor variations in the fuzzy subsets and the probability distributions involved. This ensures the robustness of our approach in handling small perturbations in the data. Finally, we provide several experimental examples to empirically validate and demonstrate the practical application of our proposed fuzzy causal inference methods.

Probabilistic Easy Variational Causal Effect

Let $X$ and $Z$ be random vectors, and $Y=g(X,Z)$. In this paper, on the one hand, for the case that $X$ and $Z$ are continuous, by using the ideas from the total variation and the flux of $g$, we develop a point of view in causal inference capable of dealing with a broad domain of causal problems. Indeed, we focus on a function, called Probabilistic Easy Variational Causal Effect (PEACE), which can measure the direct causal effect of $X$ on $Y$ with respect to continuously and interventionally changing the values of $X$ while keeping the value of $Z$ constant. PEACE is a function of $d\ge 0$, which is a degree managing the strengths of probability density values $f(x|z)$. On the other hand, we generalize the above idea for the discrete case and show its compatibility with the continuous case. Further, we investigate some properties of PEACE using measure theoretical concepts. Furthermore, we provide some identifiability criteria and several examples showing the generic capability of PEACE. We note that PEACE can deal with the causal problems for which micro-level or just macro-level changes in the value of the input variables are important. Finally, PEACE is stable under small changes in $\partial g_{in}/\partial x$ and the joint distribution of $X$ and $Z$, where $g_{in}$ is obtained from $g$ by removing all functional relationships defining $X$ and $Z$.

Probabilistic Variational Causal Effect as A new Theory for Causal Reasoning

In this paper, we introduce a new causal framework capable of dealing with probabilistic and non-probabilistic problems. Indeed, we provide a formula called Probabilistic vAriational Causal Effect (PACE). Our formula of causal effect uses the idea of total variation of a function integrated with probability theory. PACE has a parameter $d$ determining the degree of being probabilistic. The lower values of $d$ refer to the scenarios that rare cases are important. In contrast, with the higher values of $d$, our model deals with the problems that are in nature probabilistic. Hence, instead of a single value for causal effect, we provide a causal effect vector by discretizing $d$. We also address the problem of computing counterfactuals in causal reasoning. We compare our model to the Pearl model, the mutual information model, the conditional mutual information model, and the Janzing et al. model by investigating several examples.

A Fundamental Probabilistic Fuzzy Logic Framework Suitable for Causal Reasoning

In this paper, we introduce a fundamental framework to create a bridge between Probability Theory and Fuzzy Logic. Indeed, our theory formulates a random experiment of selecting crisp elements with the criterion of having a certain fuzzy attribute. To do so, we associate some specific crisp random variables to the random experiment. Then, several formulas are presented, which make it easier to compute different conditional probabilities and expected values of these random variables. Also, we provide measure theoretical basis for our probabilistic fuzzy logic framework. Note that in our theory, the probability density functions of continuous distributions which come from the aforementioned random variables include the Dirac delta function as a term. Further, we introduce an application of our theory in Causal Inference.

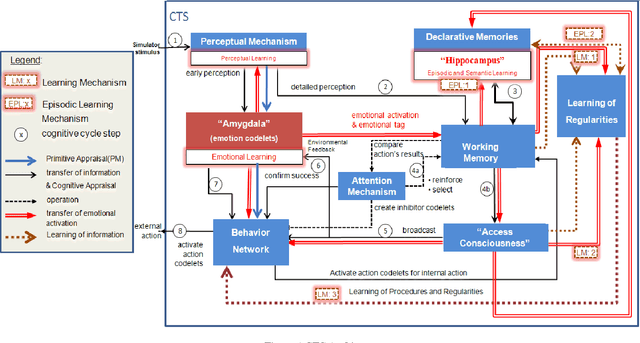
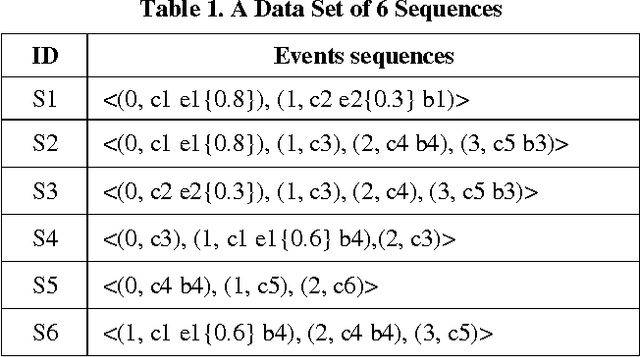
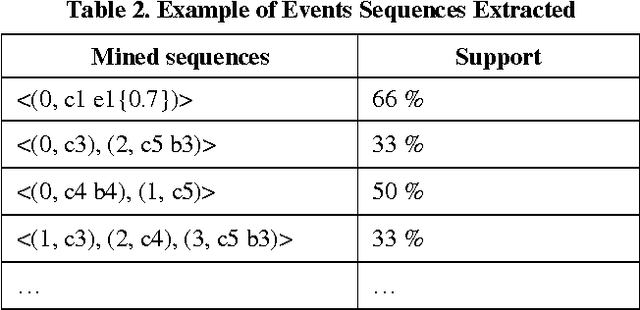
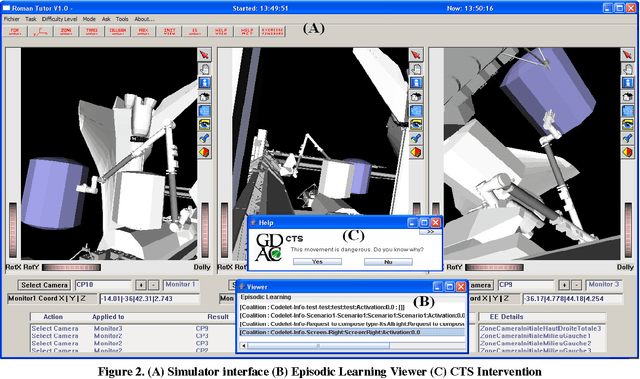
How Emotional Mechanism Helps Episodic Learning in a Cognitive Agent

In this paper we propose the CTS (Concious Tutoring System) technology, a biologically plausible cognitive agent based on human brain functions.This agent is capable of learning and remembering events and any related information such as corresponding procedures, stimuli and their emotional valences. Our proposed episodic memory and episodic learning mechanism are closer to the current multiple-trace theory in neuroscience, because they are inspired by it [5] contrary to other mechanisms that are incorporated in cognitive agents. This is because in our model emotions play a role in the encoding and remembering of events. This allows the agent to improve its behavior by remembering previously selected behaviors which are influenced by its emotional mechanism. Moreover, the architecture incorporates a realistic memory consolidation process based on a data mining algorithm.