Tzu-Chien Hsueh
Information Processing in Hybrid Photonic Electrical Reservoir Computing
Apr 01, 2024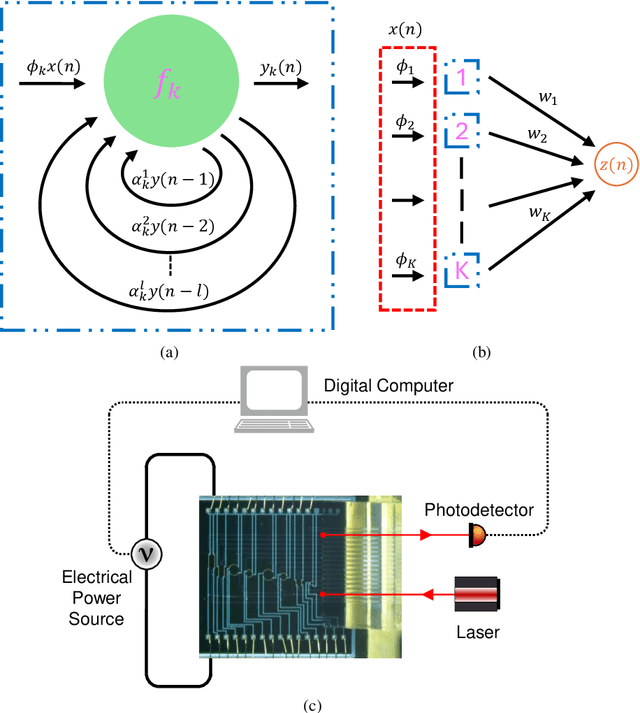
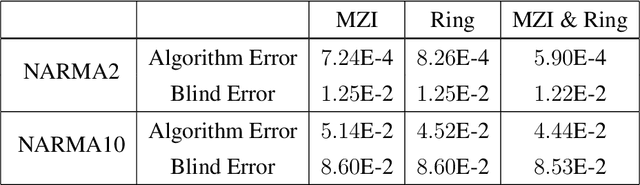
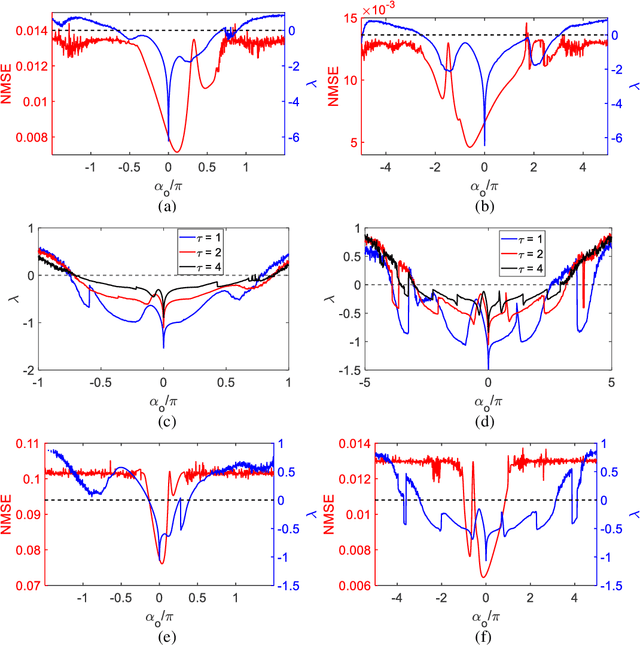
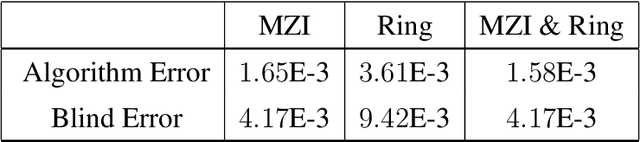
Abstract:Physical Reservoir Computing (PRC) is a recently developed variant of Neuromorphic Computing, where a pertinent physical system effectively projects information encoded in the input signal into a higher-dimensional space. While various physical hardware has demonstrated promising results for Reservoir Computing (RC), systems allowing tunability of their dynamical regimes have not received much attention regarding how to optimize relevant system parameters. In this work we employ hybrid photonic-electronic (HPE) system offering both parallelism inherent to light propagation, and electronic memory and programmable feedback allowing to induce nonlinear dynamics and tunable encoding of the photonic signal to realize HPE-RC. Specifically, we experimentally and theoretically analyze performance of integrated silicon photonic on-chip Mach-Zehnder interferometer and ring resonators with heaters acting as programmable phase modulators, controlled by detector and the feedback unit capable of realizing complex temporal dynamics of the photonic signal. Furthermore, we present an algorithm capable of predicting optimal parameters for RC by analyzing the corresponding Lyapunov exponent of the output signal and mutual information of reservoir nodes. By implementing the derived optimal parameters, we demonstrate that the corresponding resulting error of RC can be lowered by several orders of magnitude compared to a reservoir operating with randomly chosen set of parameters.
Monolithic Silicon-Photonics Linear-Algebra Accelerators Enabling Next-Gen Massive MIMO
Feb 13, 2024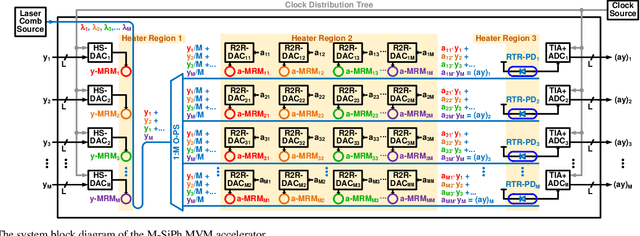
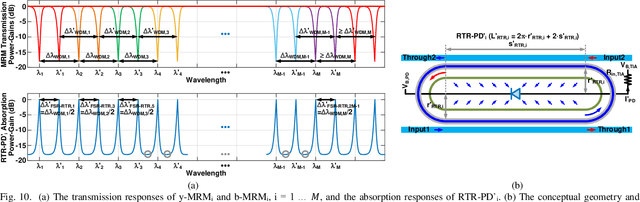
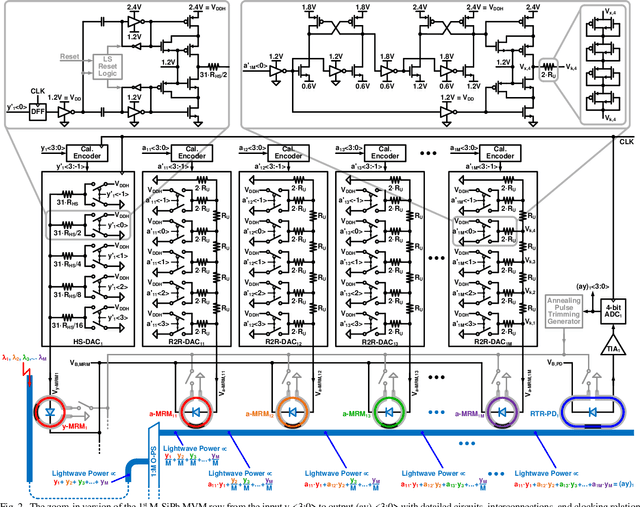
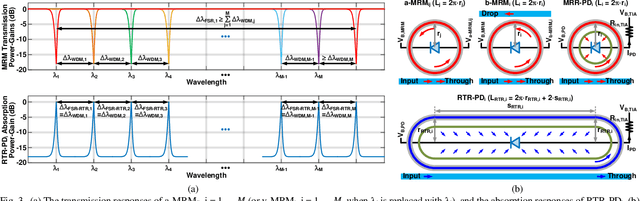
Abstract:A system-on-chip (SoC) photonic-electronic linear-algebra accelerator with the features of wavelength-division-multiplexing (WDM) based broadband photodetections and high-dimensional matrix-inversion operations fabricated in advanced monolithic silicon-photonics (M-SiPh) semiconductor process technology is proposed to achieve substantial leaps in computation density and energy efficiency, including realistic considerations of energy/area overhead due to electronic/photonic on-chip conversions, integrations, and calibrations through holistic co-design methodologies to support linear-detection based massive multiple-input multiple-output (MIMO) decoding technology requiring the inversion of channel matrices and other emergent applications limited by linear-algebra computation capacities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge