Tsonka Baitcheva
Hybrid Constructions of Binary Sequences with Low Autocorrelation Sidelobes
Apr 21, 2021



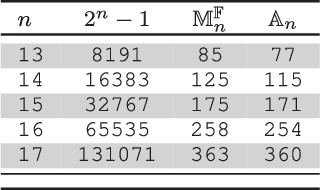
Abstract:In this work, a classical problem of the digital sequence design, or more precisely, finding binary sequences with optimal peak sidelobe level (PSL), is revisited. By combining some of our previous works, together with some mathematical insights, few hybrid heuristic algorithms were created. During our experiments, and by using the aforementioned algorithms, we were able to find PSL-optimal binary sequences for all those lengths, which were previously found during exhaustive searches by various papers throughout the literature. Then, by using a general-purpose computer, we further demonstrate the effectiveness of the proposed algorithms by revealing binary sequences with lengths between 106 and 300, the majority of which possess record-breaking PSL values. Then, by using some well-known algebraic constructions, we outline few strategies for finding highly competitive binary sequences, which could be efficiently optimized, in terms of PSL, by the proposed algorithms.
On the Generation of Long Binary Sequences with Record-Breaking PSL Values
Apr 02, 2021
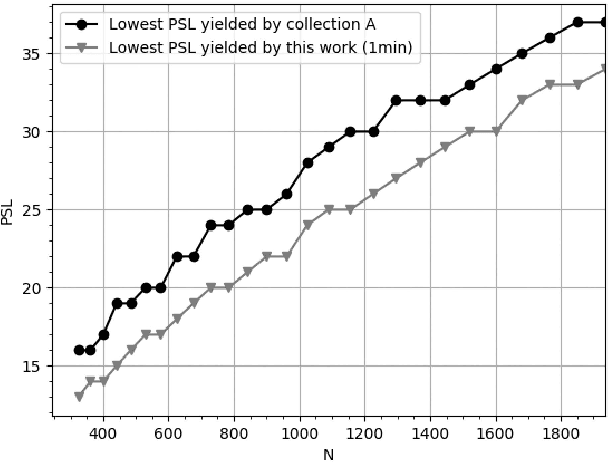
Abstract:Binary sequences are widely used in various practical fields, such as telecommunications, radar technology, navigation, cryptography, measurement sciences, biology or industry. In this paper, a method to generate long binary sequences (LBS) with low peak sidelobe level (PSL) value is proposed. Having an LBS with length $n$, both the time and memory complexities of the proposed algorithm are $\mathcal{O}(n)$. During our experiments, we repeatedly reach better PSL values than the currently known state of art constructions, such as Legendre sequences, with or without rotations, Rudin-Shapiro sequences or m-sequences, with or without rotations, by always reaching a record-breaking PSL values strictly less than $\sqrt{n}$. Furthermore, the efficiency and simplicity of the proposed method are particularly beneficial to the lightweightness of the implementation, which allowed us to reach record-breaking PSL values for less than a second.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge