A Deep Inverse-Mapping Model for a Flapping Robotic Wing

In systems control, the dynamics of a system are governed by modulating its inputs to achieve a desired outcome. For example, to control the thrust of a quad-copter propeller the controller modulates its rotation rate, relying on a straightforward mapping between the input rotation rate and the resulting thrust. This mapping can be inverted to determine the rotation rate needed to generate a desired thrust. However, in complex systems, such as flapping-wing robots where intricate fluid motions are involved, mapping inputs (wing kinematics) to outcomes (aerodynamic forces) is nontrivial and inverting this mapping for real-time control is computationally impractical. Here, we report a machine-learning solution for the inverse mapping of a flapping-wing system based on data from an experimental system we have developed. Our model learns the input wing motion required to generate a desired aerodynamic force outcome. We used a sequence-to-sequence model tailored for time-series data and augmented it with a novel adaptive-spectrum layer that implements representation learning in the frequency domain. To train our model, we developed a flapping wing system that simultaneously measures the wing's aerodynamic force and its 3D motion using high-speed cameras. We demonstrate the performance of our system on an additional open-source dataset of a flapping wing in a different flow regime. Results show superior performance compared with more complex state-of-the-art transformer-based models, with 11% improvement on the test datasets median loss. Moreover, our model shows superior inference time, making it practical for onboard robotic control. Our open-source data and framework may improve modeling and real-time control of systems governed by complex dynamics, from biomimetic robots to biomedical devices.

Conditions for energetically-optimal elasticity and their implications for biomimetic propulsion systems

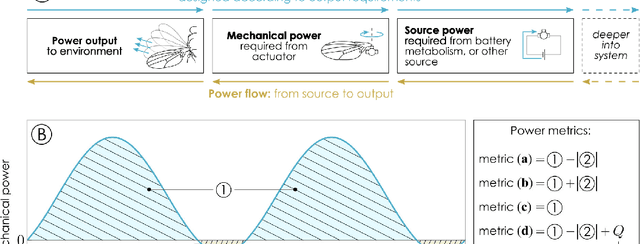
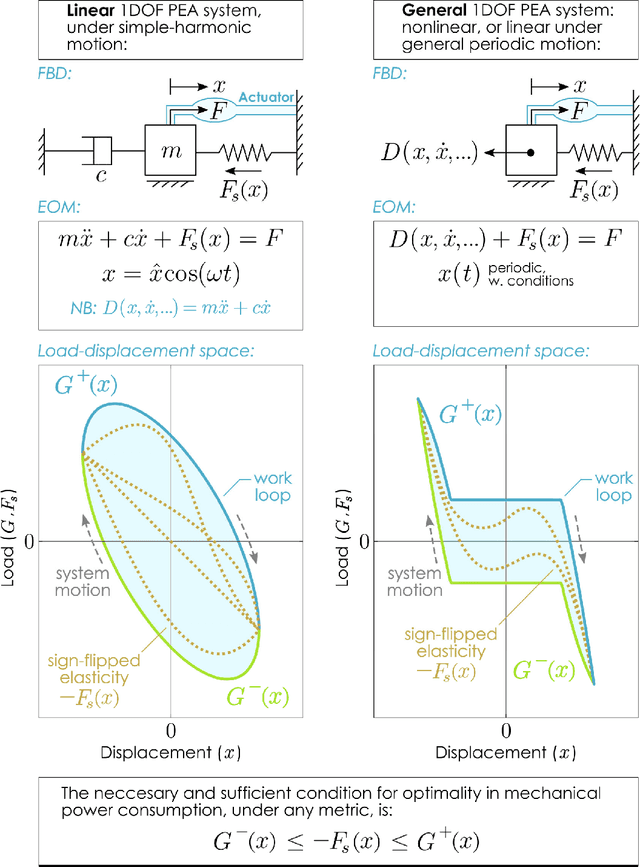
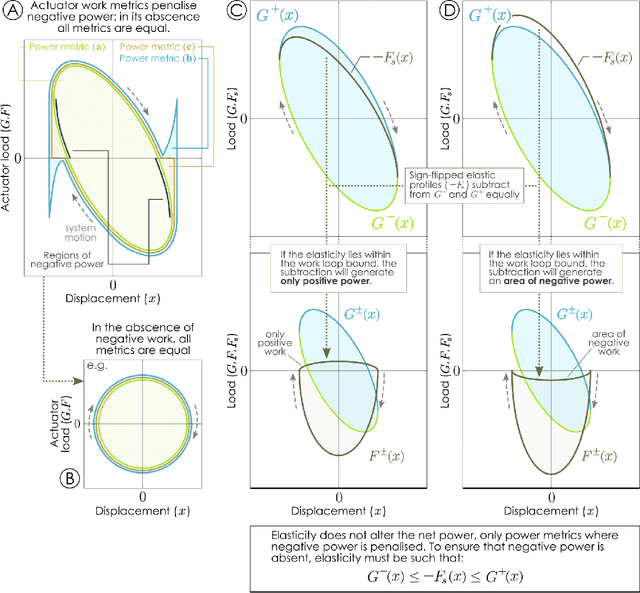
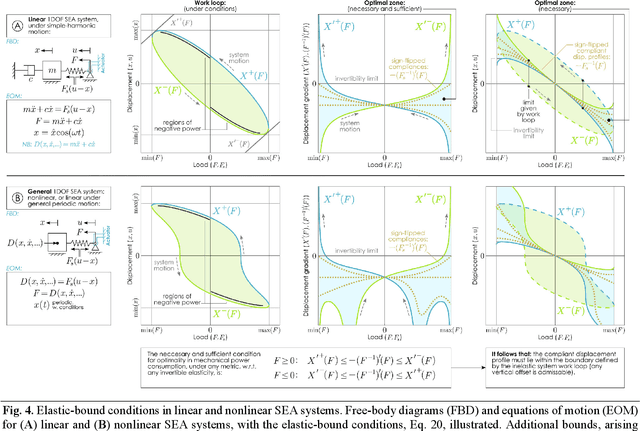
Minimising the energy consumption associated with periodic motion is a priority common to a wide range of technologies and organisms - among them, many species of flying insect, for which flapping-wing flight is a life-essential mode of locomotion. In pursuit of this priority, the following problem often manifests: how to introduce elasticity into an actuated, oscillating, system in order to minimise actuator power consumption? Here, we explore this question in a range of general systems, and find some surprising answers. For instance, it is widely assumed that, if the system dynamics are linear, then linear resonant elasticity is the only optimal choice. We show, to the contrary, that there exist nonlinear elasticities with equivalent optimality, and provide an elegant method for constructing these elasticities in general systems. This is a new principle of linear and nonlinear dynamics, fundamentally altering how questions of energetic optimality in a wide range of dynamical systems must be approached. Furthermore, we show how this principle enables new forms of optimal system design, including optimal unidirectional actuation in nonlinear systems; new tools for the design of optimal biomimetic propulsion systems; and new insights into the role of structural elasticity in a range of different organisms.