On Finite Entailment of Non-Local Queries in Description Logics

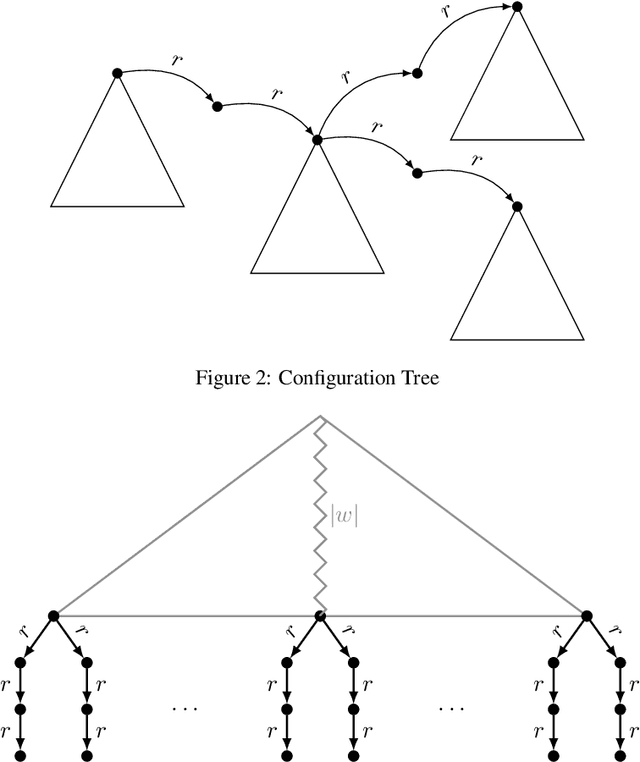
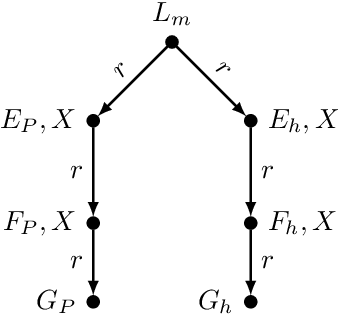
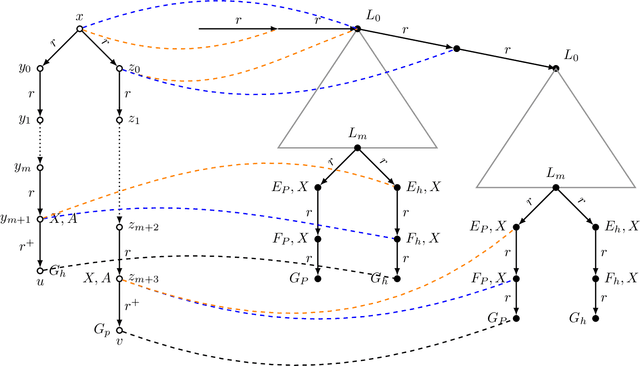
We study the problem of finite entailment of ontology-mediated queries. Going beyond local queries, we allow transitive closure over roles. We focus on ontologies formulated in the description logics ALCOI and ALCOQ, extended with transitive closure. For both logics, we show 2EXPTIME upper bounds for finite entailment of unions of conjunctive queries with transitive closure. We also provide a matching lower bound by showing that finite entailment of conjunctive queries with transitive closure in ALC is 2EXPTIME-hard.

Finite Query Answering in Expressive Description Logics with Transitive Roles

We study the problem of finite ontology mediated query answering (FOMQA), the variant of OMQA where the represented world is assumed to be finite, and thus only finite models of the ontology are considered. We adopt the most typical setting with unions of conjunctive queries and ontologies expressed in description logics (DLs). The study of FOMQA is relevant in settings that are not finitely controllable. This is the case not only for DLs without the finite model property, but also for those allowing transitive role declarations. When transitive roles are allowed, evaluating queries is challenging: FOMQA is undecidable for SHOIF and only known to be decidable for the Horn fragment of ALCIF. We show decidability of FOMQA for three proper fragments of SOIF: SOI, SOF, and SIF. Our approach is to characterise models relevant for deciding finite query entailment. Relying on a certain regularity of these models, we develop automata-based decision procedures with optimal complexity bounds.