Smart Cubing for Graph Search: A Comparative Study

Parallel solving via cube-and-conquer is a key method for scaling SAT solvers to hard instances. While cube-and-conquer has proven successful for pure SAT problems, notably the Pythagorean triples conjecture, its application to SAT solvers extended with propagators presents unique challenges, as these propagators learn constraints dynamically during the search. We study this problem using SAT Modulo Symmetries (SMS) as our primary test case, where a symmetry-breaking propagator reduces the search space by learning constraints that eliminate isomorphic graphs. Through extensive experimentation comprising over 10,000 CPU hours, we systematically evaluate different cube-and-conquer variants on three well-studied combinatorial problems. Our methodology combines prerun phases to collect learned constraints, various cubing strategies, and parameter tuning via algorithm configuration and LLM-generated design suggestions. The comprehensive empirical evaluation provides new insights into effective cubing strategies for propagator-based SAT solving, with our best method achieving speedups of 2-3x from improved cubing and parameter tuning, providing an additional 1.5-2x improvement on harder instances.

Co-Certificate Learning with SAT Modulo Symmetries

We present a new SAT-based method for generating all graphs up to isomorphism that satisfy a given co-NP property. Our method extends the SAT Modulo Symmetry (SMS) framework with a technique that we call co-certificate learning. If SMS generates a candidate graph that violates the given co-NP property, we obtain a certificate for this violation, i.e., `co-certificate' for the co-NP property. The co-certificate gives rise to a clause that the SAT solver, serving as SMS's backend, learns as part of its CDCL procedure. We demonstrate that SMS plus co-certificate learning is a powerful method that allows us to improve the best-known lower bound on the size of Kochen-Specker vector systems, a problem that is central to the foundations of quantum mechanics and has been studied for over half a century. Our approach is orders of magnitude faster and scales significantly better than a recently proposed SAT-based method.

Are Hitting Formulas Hard for Resolution?

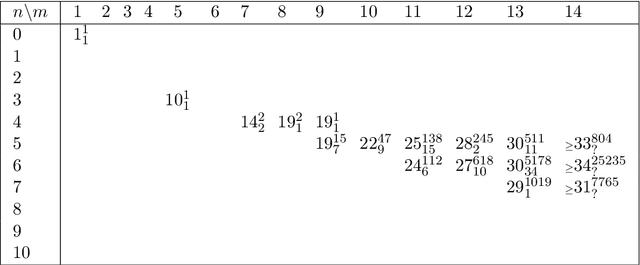
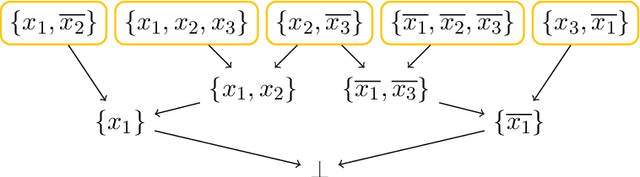
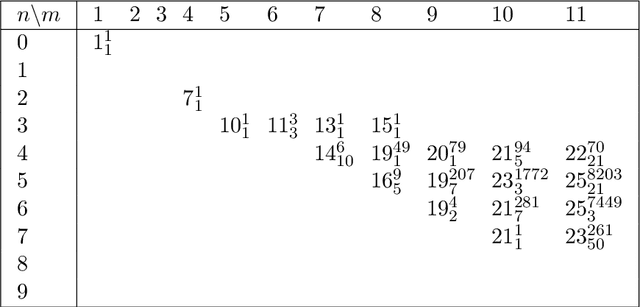
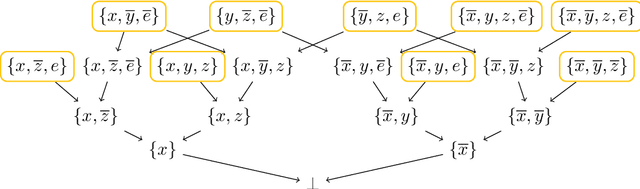
Hitting formulas, introduced by Iwama, are an unusual class of propositional CNF formulas. Not only is their satisfiability decidable in polynomial time, but even their models can be counted in closed form. This stands in stark contrast with other polynomial-time decidable classes, which usually have algorithms based on backtracking and resolution and for which model counting remains hard, like 2-SAT and Horn-SAT. However, those resolution-based algorithms usually easily imply an upper bound on resolution complexity, which is missing for hitting formulas. Are hitting formulas hard for resolution? In this paper we take the first steps towards answering this question. We show that the resolution complexity of hitting formulas is dominated by so-called irreducible hitting formulas, first studied by Kullmann and Zhao, that cannot be composed of smaller hitting formulas. However, by definition, large irreducible unsatisfiable hitting formulas are difficult to construct; it is not even known whether infinitely many exist. Building upon our theoretical results, we implement an efficient algorithm on top of the Nauty software package to enumerate all irreducible unsatisfiable hitting formulas with up to 14 clauses. We also determine the exact resolution complexity of the generated hitting formulas with up to 13 clauses by extending a known SAT encoding for our purposes. Our experimental results suggest that hitting formulas are indeed hard for resolution.