Are Hitting Formulas Hard for Resolution?
Paper and Code
Jun 30, 2022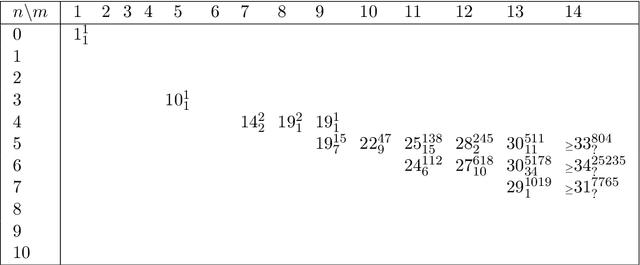
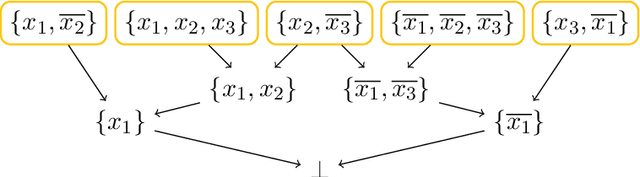
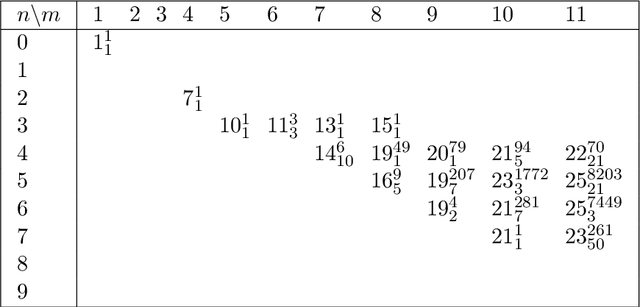
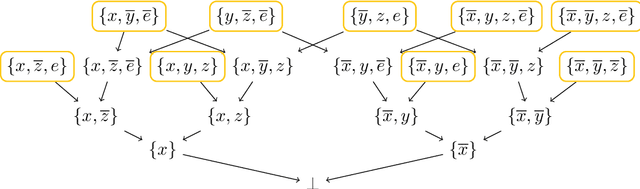
Hitting formulas, introduced by Iwama, are an unusual class of propositional CNF formulas. Not only is their satisfiability decidable in polynomial time, but even their models can be counted in closed form. This stands in stark contrast with other polynomial-time decidable classes, which usually have algorithms based on backtracking and resolution and for which model counting remains hard, like 2-SAT and Horn-SAT. However, those resolution-based algorithms usually easily imply an upper bound on resolution complexity, which is missing for hitting formulas. Are hitting formulas hard for resolution? In this paper we take the first steps towards answering this question. We show that the resolution complexity of hitting formulas is dominated by so-called irreducible hitting formulas, first studied by Kullmann and Zhao, that cannot be composed of smaller hitting formulas. However, by definition, large irreducible unsatisfiable hitting formulas are difficult to construct; it is not even known whether infinitely many exist. Building upon our theoretical results, we implement an efficient algorithm on top of the Nauty software package to enumerate all irreducible unsatisfiable hitting formulas with up to 14 clauses. We also determine the exact resolution complexity of the generated hitting formulas with up to 13 clauses by extending a known SAT encoding for our purposes. Our experimental results suggest that hitting formulas are indeed hard for resolution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge