Towards Foundational Models for Dynamical System Reconstruction: Hierarchical Meta-Learning via Mixture of Experts

As foundational models reshape scientific discovery, a bottleneck persists in dynamical system reconstruction (DSR): the ability to learn across system hierarchies. Many meta-learning approaches have been applied successfully to single systems, but falter when confronted with sparse, loosely related datasets requiring multiple hierarchies to be learned. Mixture of Experts (MoE) offers a natural paradigm to address these challenges. Despite their potential, we demonstrate that naive MoEs are inadequate for the nuanced demands of hierarchical DSR, largely due to their gradient descent-based gating update mechanism which leads to slow updates and conflicted routing during training. To overcome this limitation, we introduce MixER: Mixture of Expert Reconstructors, a novel sparse top-1 MoE layer employing a custom gating update algorithm based on $K$-means and least squares. Extensive experiments validate MixER's capabilities, demonstrating efficient training and scalability to systems of up to ten parametric ordinary differential equations. However, our layer underperforms state-of-the-art meta-learners in high-data regimes, particularly when each expert is constrained to process only a fraction of a dataset composed of highly related data points. Further analysis with synthetic and neuroscientific time series suggests that the quality of the contextual representations generated by MixER is closely linked to the presence of hierarchical structure in the data.

Extending Contextual Self-Modulation: Meta-Learning Across Modalities, Task Dimensionalities, and Data Regimes

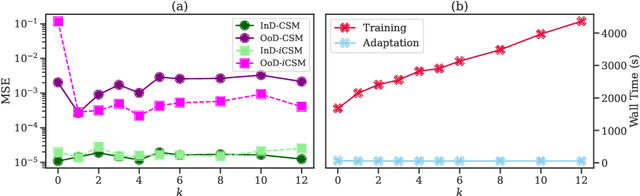
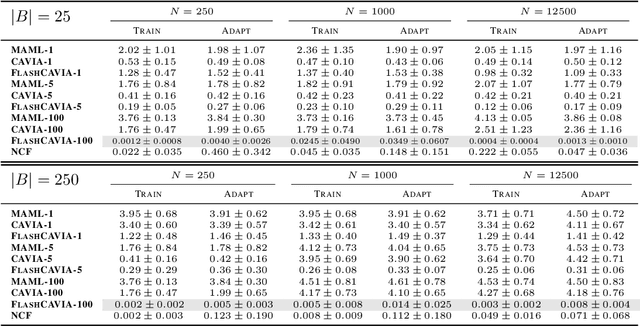
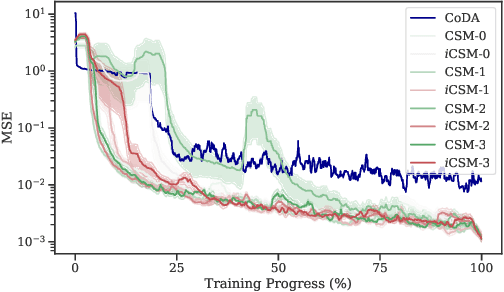
Contextual Self-Modulation (CSM) is a potent regularization mechanism for the Neural Context Flow (NCF) framework which demonstrates powerful meta-learning of physical systems. However, CSM has limitations in its applicability across different modalities and in high-data regimes. In this work, we introduce two extensions: $i$CSM, which expands CSM to infinite-dimensional tasks, and StochasticNCF, which improves scalability. These extensions are demonstrated through comprehensive experimentation on a range of tasks, including dynamical systems with parameter variations, computer vision challenges, and curve fitting problems. $i$CSM embeds the contexts into an infinite-dimensional function space, as opposed to CSM which uses finite-dimensional context vectors. StochasticNCF enables the application of both CSM and $i$CSM to high-data scenarios by providing an unbiased approximation of meta-gradient updates through a sampled set of nearest environments. Additionally, we incorporate higher-order Taylor expansions via Taylor-Mode automatic differentiation, revealing that higher-order approximations do not necessarily enhance generalization. Finally, we demonstrate how CSM can be integrated into other meta-learning frameworks with FlashCAVIA, a computationally efficient extension of the CAVIA meta-learning framework (Zintgraf et al. 2019). FlashCAVIA outperforms its predecessor across various benchmarks and reinforces the utility of bi-level optimization techniques. Together, these contributions establish a robust framework for tackling an expanded spectrum of meta-learning tasks, offering practical insights for out-of-distribution generalization. Our open-sourced library, designed for flexible integration of self-modulation into contextual meta-learning workflows, is available at \url{github.com/ddrous/self-mod}.

Neural Context Flows for Learning Generalizable Dynamical Systems

Neural Ordinary Differential Equations typically struggle to generalize to new dynamical behaviors created by parameter changes in the underlying system, even when the dynamics are close to previously seen behaviors. The issue gets worse when the changing parameters are unobserved, i.e., their value or influence is not directly measurable when collecting data. We introduce Neural Context Flow (NCF), a framework that encodes said unobserved parameters in a latent context vector as input to a vector field. NCFs leverage differentiability of the vector field with respect to the parameters, along with first-order Taylor expansion to allow any context vector to influence trajectories from other parameters. We validate our method and compare it to established Multi-Task and Meta-Learning alternatives, showing competitive performance in mean squared error for in-domain and out-of-distribution evaluation on the Lotka-Volterra, Glycolytic Oscillator, and Gray-Scott problems. This study holds practical implications for foundational models in science and related areas that benefit from conditional neural ODEs. Our code is openly available at https://github.com/ddrous/ncflow.

A Comparison of Mesh-Free Differentiable Programming and Data-Driven Strategies for Optimal Control under PDE Constraints

The field of Optimal Control under Partial Differential Equations (PDE) constraints is rapidly changing under the influence of Deep Learning and the accompanying automatic differentiation libraries. Novel techniques like Physics-Informed Neural Networks (PINNs) and Differentiable Programming (DP) are to be contrasted with established numerical schemes like Direct-Adjoint Looping (DAL). We present a comprehensive comparison of DAL, PINN, and DP using a general-purpose mesh-free differentiable PDE solver based on Radial Basis Functions. Under Laplace and Navier-Stokes equations, we found DP to be extremely effective as it produces the most accurate gradients; thriving even when DAL fails and PINNs struggle. Additionally, we provide a detailed benchmark highlighting the limited conditions under which any of those methods can be efficiently used. Our work provides a guide to Optimal Control practitioners and connects them further to the Deep Learning community.