Learnable & Interpretable Model Combination in Dynamic Systems Modeling

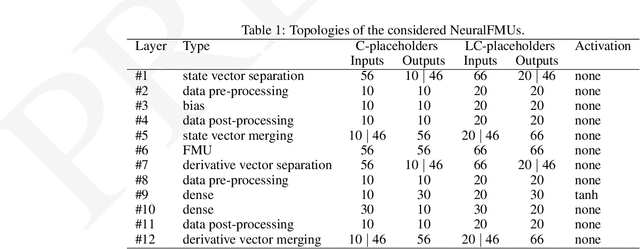
One of the core concepts in science, and something that happens intuitively in every-day dynamic systems modeling, is the combination of models or methods. Especially in dynamical systems modeling, often two or more structures are combined to obtain a more powerful or efficient architecture regarding a specific application (area). Further, even physical simulations are combined with machine learning architectures, to increase prediction accuracy or optimize the computational performance. In this work, we shortly discuss, which types of models are usually combined and propose a model interface that is capable of expressing a width variety of mixed algebraic, discrete and differential equation based models. Further, we examine different established, as well as new ways of combining these models from a system theoretical point of view and highlight two challenges - algebraic loops and local event affect functions in discontinuous models - that require a special approach. Finally, we propose a new wildcard topology, that is capable of describing the generic connection between two combined models in an easy to interpret fashion that can be learned as part of a gradient based optimization procedure. The contributions of this paper are highlighted at a proof of concept: Different connection topologies between two models are learned, interpreted and compared applying the proposed methodology and software implementation.

Eigen-informed NeuralODEs: Dealing with stability and convergence issues of NeuralODEs

Using vanilla NeuralODEs to model large and/or complex systems often fails due two reasons: Stability and convergence. NeuralODEs are capable of describing stable as well as instable dynamic systems. Selecting an appropriate numerical solver is not trivial, because NeuralODE properties change during training. If the NeuralODE becomes more stiff, a suboptimal solver may need to perform very small solver steps, which significantly slows down the training process. If the NeuralODE becomes to instable, the numerical solver might not be able to solve it at all, which causes the training process to terminate. Often, this is tackled by choosing a computational expensive solver that is robust to instable and stiff ODEs, but at the cost of a significantly decreased training performance. Our method on the other hand, allows to enforce ODE properties that fit a specific solver or application-related boundary conditions. Concerning the convergence behavior, NeuralODEs often tend to run into local minima, especially if the system to be learned is highly dynamic and/or oscillating over multiple periods. Because of the vanishing gradient at a local minimum, the NeuralODE is often not capable of leaving it and converge to the right solution. We present a technique to add knowledge of ODE properties based on eigenvalues - like (partly) stability, oscillation capability, frequency, damping and/or stiffness - to the training objective of a NeuralODE. We exemplify our method at a linear as well as a nonlinear system model and show, that the presented training process is far more robust against local minima, instabilities and sparse data samples and improves training convergence and performance.

NeuralFMU: Presenting a workflow for integrating hybrid NeuralODEs into real world applications

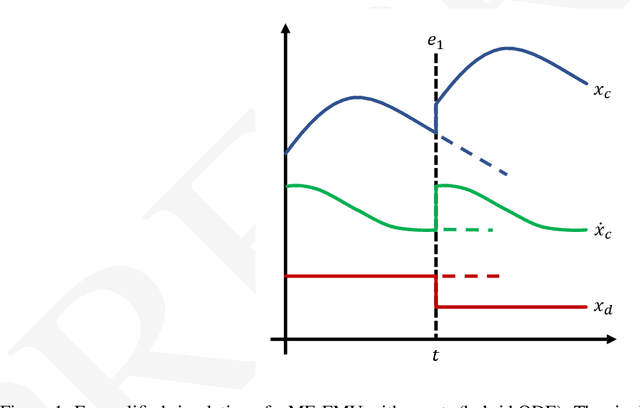
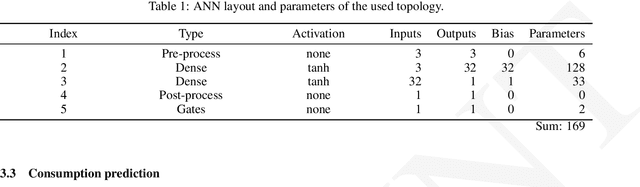
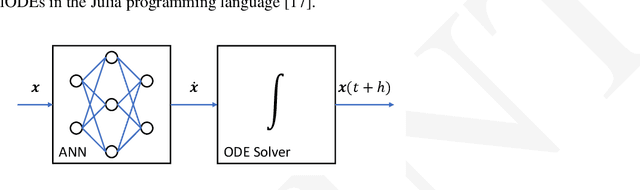
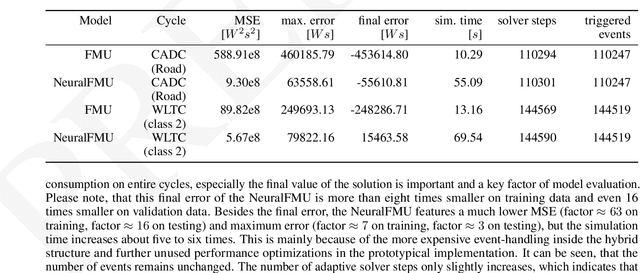
The term NeuralODE describes the structural combination of an Artifical Neural Network (ANN) and a numerical solver for Ordinary Differential Equations (ODEs), the former acts as the right-hand side of the ODE to be solved. This concept was further extended by a black-box model in the form of a Functional Mock-up Unit (FMU) to obtain a subclass of NeuralODEs, named NeuralFMUs. The resulting structure features the advantages of first-principle and data-driven modeling approaches in one single simulation model: A higher prediction accuracy compared to conventional First Principle Models (FPMs), while also a lower training effort compared to purely data-driven models. We present an intuitive workflow to setup and use NeuralFMUs, enabling the encapsulation and reuse of existing conventional models exported from common modeling tools. Moreover, we exemplify this concept by deploying a NeuralFMU for a consumption simulation based on a Vehicle Longitudinal Dynamics Model (VLDM), which is a typical use case in automotive industry. Related challenges that are often neglected in scientific use cases, like real measurements (e.g. noise), an unknown system state or high-frequent discontinuities, are handled in this contribution. For the aim to build a hybrid model with a higher prediction quality than the original FPM, we briefly highlight two open-source libraries: FMI.jl for integrating FMUs into the Julia programming environment, as well as an extension to this library called FMIFlux.jl, that allows for the integration of FMUs into a neural network topology to finally obtain a NeuralFMU.

Hybrid modeling of the human cardiovascular system using NeuralFMUs

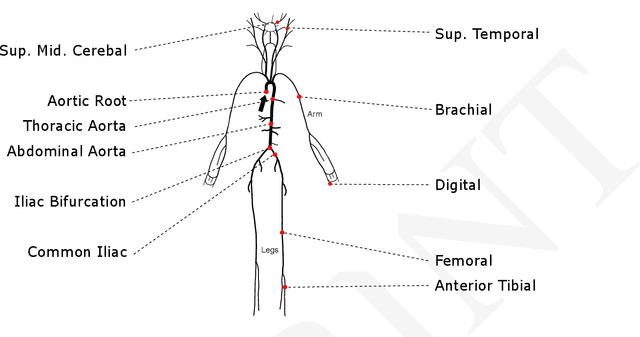
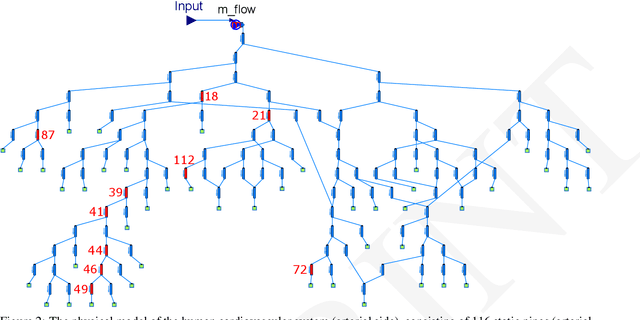
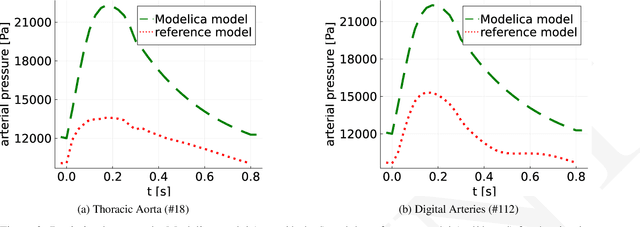
Hybrid modeling, the combination of first principle and machine learning models, is an emerging research field that gathers more and more attention. Even if hybrid models produce formidable results for academic examples, there are still different technical challenges that hinder the use of hybrid modeling in real-world applications. By presenting NeuralFMUs, the fusion of a FMU, a numerical ODE solver and an ANN, we are paving the way for the use of a variety of first principle models from different modeling tools as parts of hybrid models. This contribution handles the hybrid modeling of a complex, real-world example: Starting with a simplified 1D-fluid model of the human cardiovascular system (arterial side), the aim is to learn neglected physical effects like arterial elasticity from data. We will show that the hybrid modeling process is more comfortable, needs less system knowledge and is therefore less error-prone compared to modeling solely based on first principle. Further, the resulting hybrid model has improved in computation performance, compared to a pure first principle white-box model, while still fulfilling the requirements regarding accuracy of the considered hemodynamic quantities. The use of the presented techniques is explained in a general manner and the considered use-case can serve as example for other modeling and simulation applications in and beyond the medical domain.

NeuralFMU: Towards Structural Integration of FMUs into Neural Networks

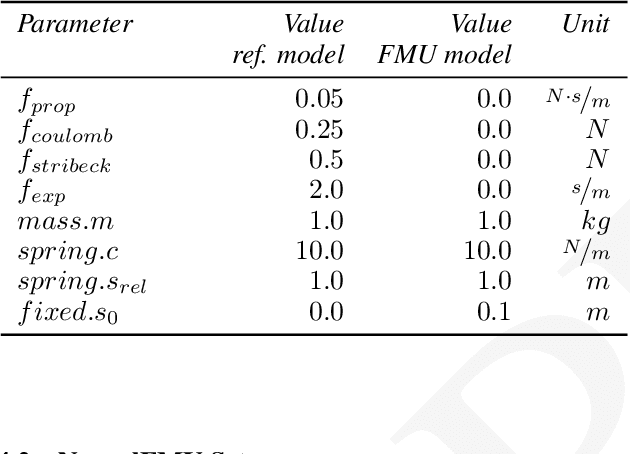
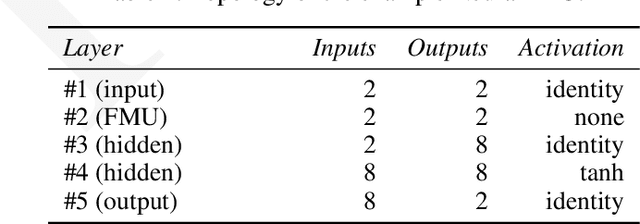
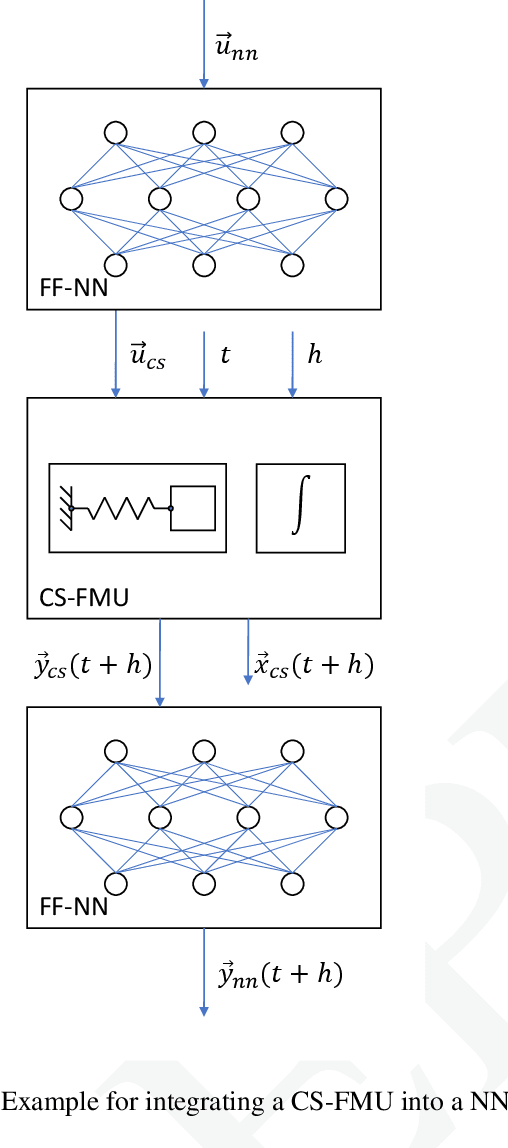
This paper covers two major subjects: First, the presentation of a new open-source library called FMI.jl for integrating FMI into the Julia programming environment by providing the possibility to load, parameterize and simulate FMUs. Further, an extension to this library called FMIFlux.jl is introduced, that allows the integration of FMUs into a neural network topology to obtain a NeuralFMU. This structural combination of an industry typical black-box model and a data-driven machine learning model combines the different advantages of both modeling approaches in one single development environment. This allows for the usage of advanced data driven modeling techniques for physical effects that are difficult to model based on first principles.