Data-driven detector signal characterization with constrained bottleneck autoencoders

A common technique in high energy physics is to characterize the response of a detector by means of models tunned to data which build parametric maps from the physical parameters of the system to the expected signal of the detector. When the underlying model is unknown it is difficult to apply this method, and often, simplifying assumptions are made introducing modeling errors. In this article, using a waveform toy model we present how deep learning in the form of constrained bottleneck autoencoders can be used to learn the underlying unknown detector response model directly from data. The results show that excellent performance results can be achieved even when the signals are significantly affected by random noise. The trained algorithm can be used simultaneously to perform estimations on the physical parameters of the model, simulate the detector response with high fidelity and to denoise detector signals.

Exhaustive Neural Importance Sampling applied to Monte Carlo event generation

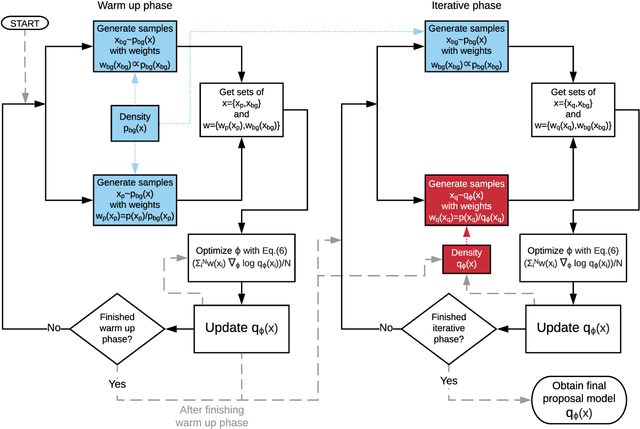
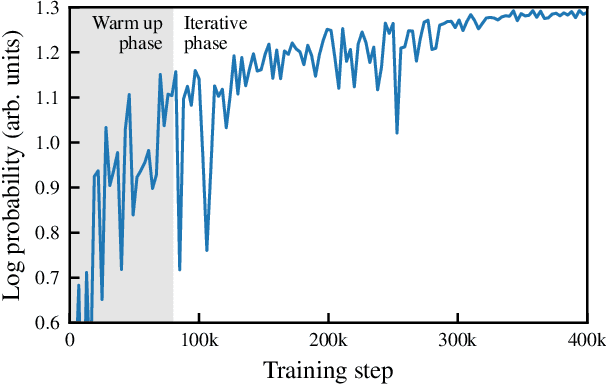
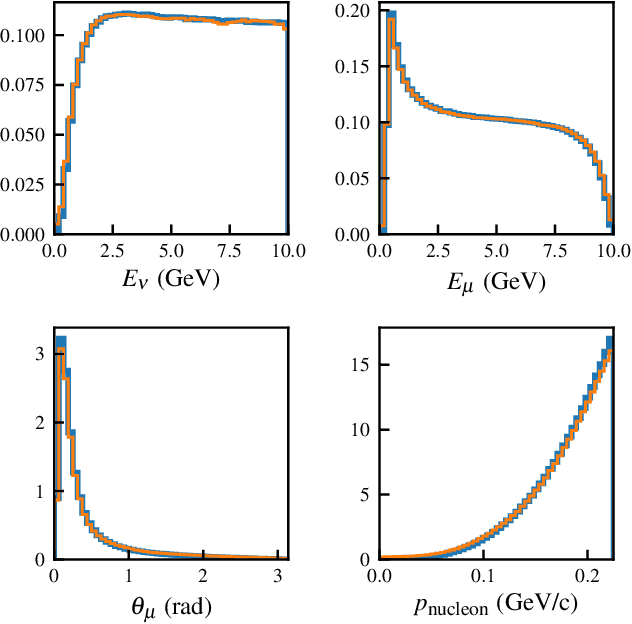
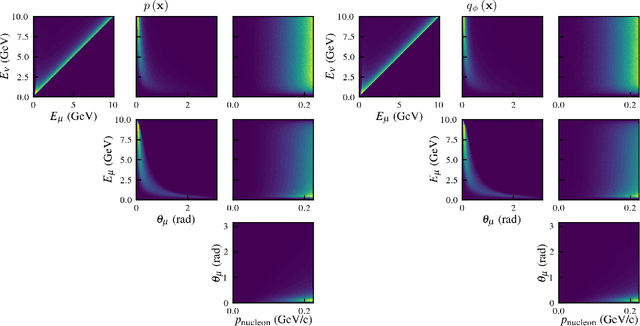
The generation of accurate neutrino-nucleus cross-section models needed for neutrino oscillation experiments require simultaneously the description of many degrees of freedom and precise calculations to model nuclear responses. The detailed calculation of complete models makes the Monte Carlo generators slow and impractical. We present Exhaustive Neural Importance Sampling (ENIS), a method based on normalizing flows to find a suitable proposal density for rejection sampling automatically and efficiently, and discuss how this technique solves common issues of the rejection algorithm.

Efficient sampling generation from explicit densities via Normalizing Flows

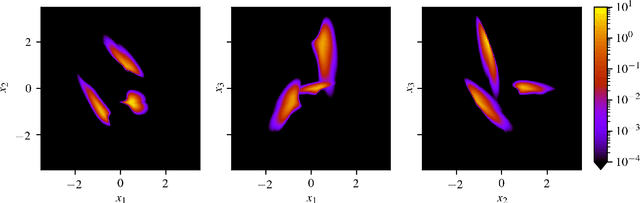
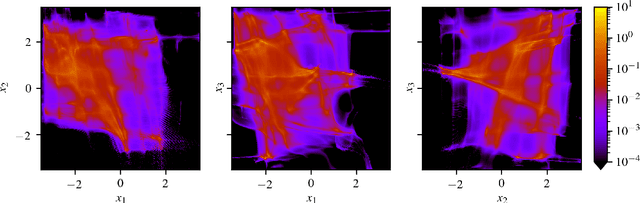
For many applications, such as computing the expected value of different magnitudes, sampling from a known probability density function, the target density, is crucial but challenging through the inverse transform. In these cases, rejection and importance sampling require suitable proposal densities, which can be evaluated and sampled from efficiently. We will present a method based on normalizing flows, proposing a solution for the common problem of exploding reverse Kullback-Leibler divergence due to the target density having values of 0 in regions of the flow transformation. The performance of the method will be demonstrated using a multi-mode complex density function.