Justifications in Constraint Handling Rules for Logical Retraction in Dynamic Algorithms

We present a straightforward source-to-source transformation that introduces justifications for user-defined constraints into the CHR programming language. Then a scheme of two rules suffices to allow for logical retraction (deletion, removal) of constraints during computation. Without the need to recompute from scratch, these rules remove not only the constraint but also undo all consequences of the rule applications that involved the constraint. We prove a confluence result concerning the rule scheme and show its correctness. When algorithms are written in CHR, constraints represent both data and operations. CHR is already incremental by nature, i.e. constraints can be added at runtime. Logical retraction adds decrementality. Hence any algorithm written in CHR with justifications will become fully dynamic. Operations can be undone and data can be removed at any point in the computation without compromising the correctness of the result. We present two classical examples of dynamic algorithms, written in our prototype implementation of CHR with justifications that is available online: maintaining the minimum of a changing set of numbers and shortest paths in a graph whose edges change.

Theory of Finite or Infinite Trees Revisited

We present in this paper a first-order axiomatization of an extended theory $T$ of finite or infinite trees, built on a signature containing an infinite set of function symbols and a relation $\fini(t)$ which enables to distinguish between finite or infinite trees. We show that $T$ has at least one model and prove its completeness by giving not only a decision procedure, but a full first-order constraint solver which gives clear and explicit solutions for any first-order constraint satisfaction problem in $T$. The solver is given in the form of 16 rewriting rules which transform any first-order constraint $\phi$ into an equivalent disjunction $\phi$ of simple formulas such that $\phi$ is either the formula $\true$ or the formula $\false$ or a formula having at least one free variable, being equivalent neither to $\true$ nor to $\false$ and where the solutions of the free variables are expressed in a clear and explicit way. The correctness of our rules implies the completeness of $T$. We also describe an implementation of our algorithm in CHR (Constraint Handling Rules) and compare the performance with an implementation in C++ and that of a recent decision procedure for decomposable theories.

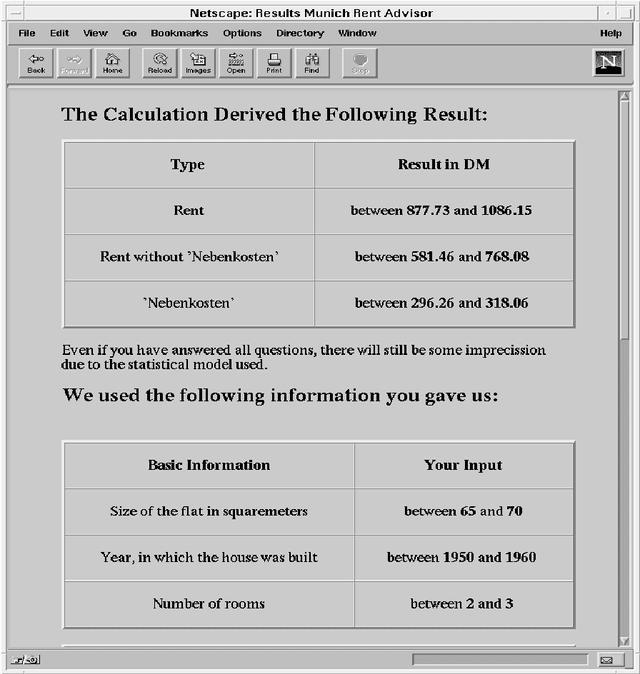
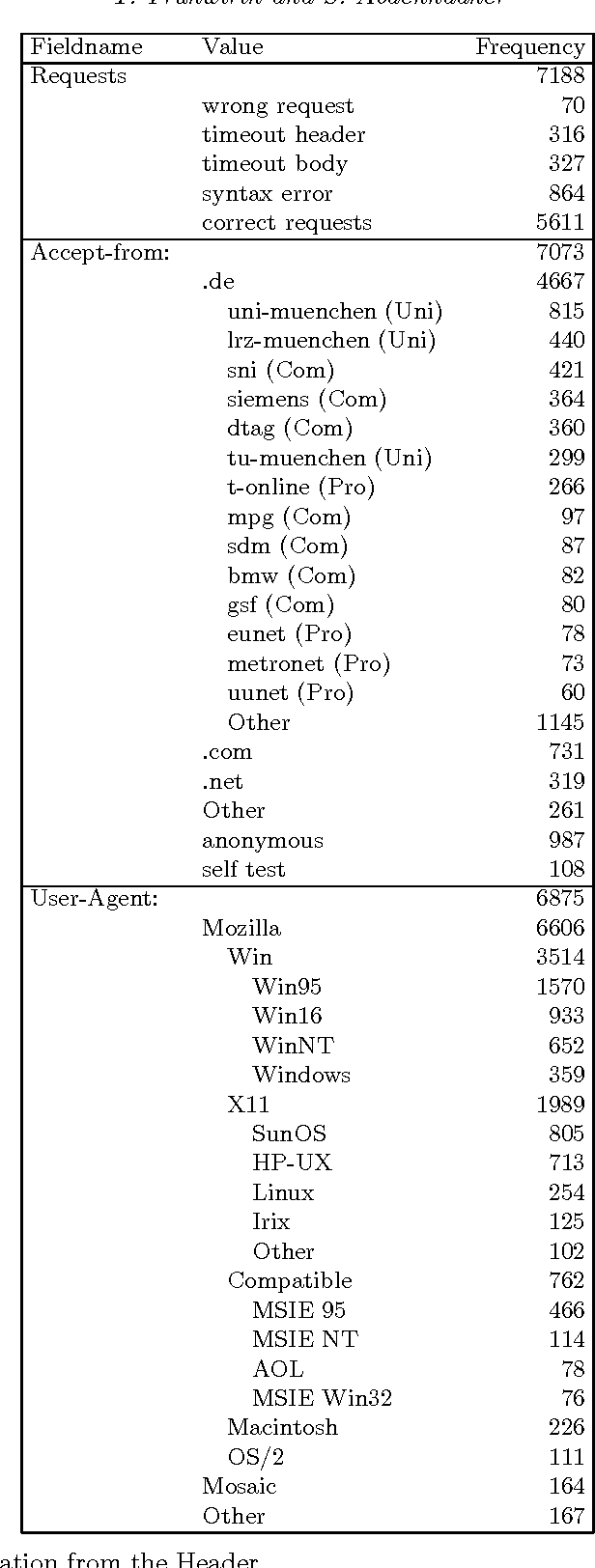
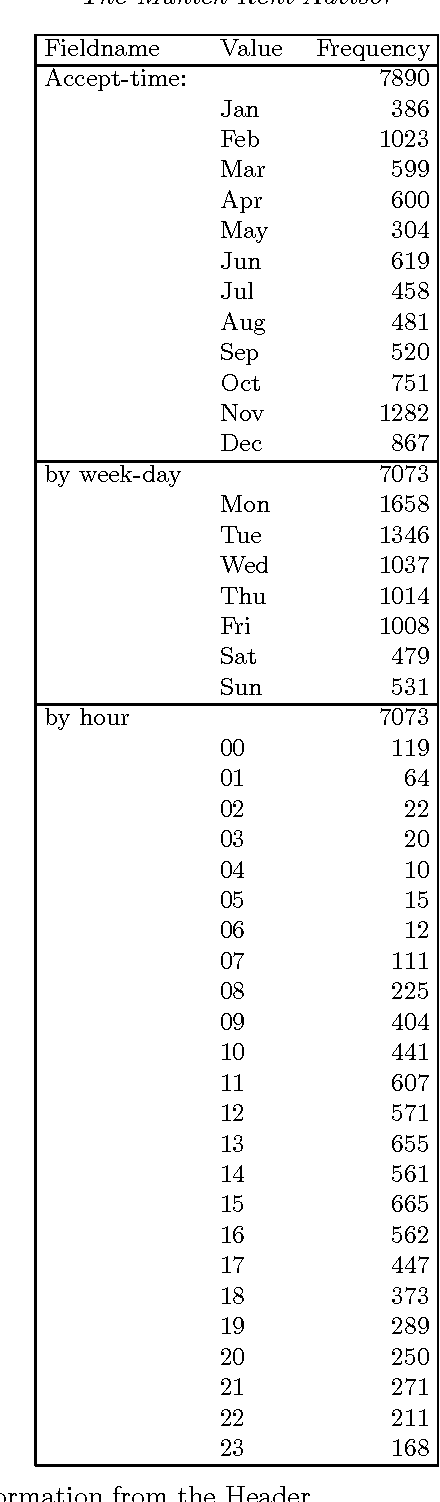
The Munich Rent Advisor: A Success for Logic Programming on the Internet

Most cities in Germany regularly publish a booklet called the {\em Mietspiegel}. It basically contains a verbal description of an expert system. It allows the calculation of the estimated fair rent for a flat. By hand, one may need a weekend to do so. With our computerized version, the {\em Munich Rent Advisor}, the user just fills in a form in a few minutes and the rent is calculated immediately. We also extended the functionality and applicability of the {\em Mietspiegel} so that the user need not answer all questions on the form. The key to computing with partial information using high-level programming was to use constraint logic programming. We rely on the internet, and more specifically the World Wide Web, to provide this service to a broad user group. More than ten thousand people have used our service in the last three years. This article describes the experiences in implementing and using the {\em Munich Rent Advisor}. Our results suggests that logic programming with constraints can be an important ingredient in intelligent internet systems.