A foundation for exact binarized morphological neural networks

Training and running deep neural networks (NNs) often demands a lot of computation and energy-intensive specialized hardware (e.g. GPU, TPU...). One way to reduce the computation and power cost is to use binary weight NNs, but these are hard to train because the sign function has a non-smooth gradient. We present a model based on Mathematical Morphology (MM), which can binarize ConvNets without losing performance under certain conditions, but these conditions may not be easy to satisfy in real-world scenarios. To solve this, we propose two new approximation methods and develop a robust theoretical framework for ConvNets binarization using MM. We propose as well regularization losses to improve the optimization. We empirically show that our model can learn a complex morphological network, and explore its performance on a classification task.

Binary Multi Channel Morphological Neural Network

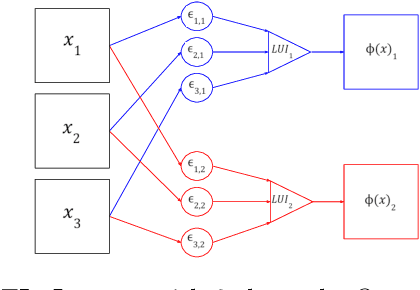
Neural networks and particularly Deep learning have been comparatively little studied from the theoretical point of view. Conversely, Mathematical Morphology is a discipline with solid theoretical foundations. We combine these domains to propose a new type of neural architecture that is theoretically more explainable. We introduce a Binary Morphological Neural Network (BiMoNN) built upon the convolutional neural network. We design it for learning morphological networks with binary inputs and outputs. We demonstrate an equivalence between BiMoNNs and morphological operators that we can use to binarize entire networks. These can learn classical morphological operators and show promising results on a medical imaging application.

Binary Morphological Neural Network

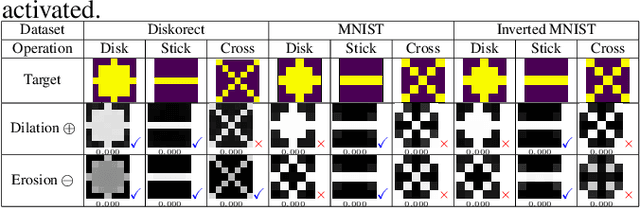
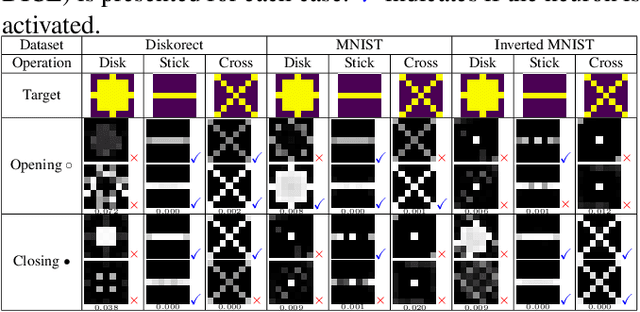
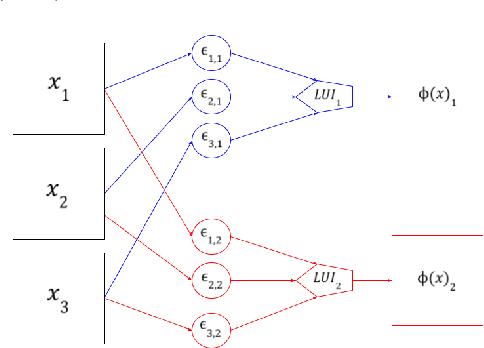
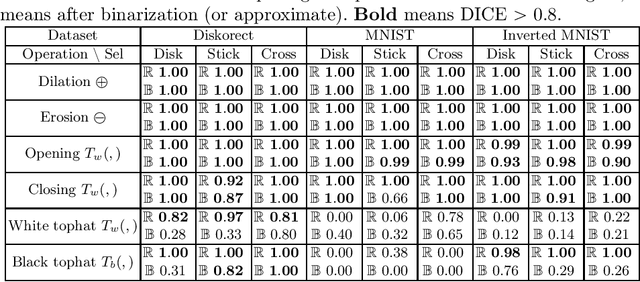
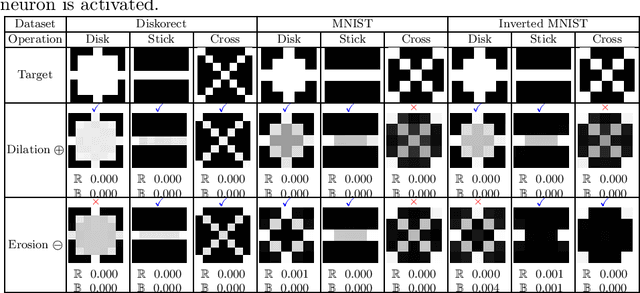
In the last ten years, Convolutional Neural Networks (CNNs) have formed the basis of deep-learning architectures for most computer vision tasks. However, they are not necessarily optimal. For example, mathematical morphology is known to be better suited to deal with binary images. In this work, we create a morphological neural network that handles binary inputs and outputs. We propose their construction inspired by CNNs to formulate layers adapted to such images by replacing convolutions with erosions and dilations. We give explainable theoretical results on whether or not the resulting learned networks are indeed morphological operators. We present promising experimental results designed to learn basic binary operators, and we have made our code publicly available online.