Extrapolative ML Models for Copolymers

Machine learning models have been progressively used for predicting materials properties. These models can be built using pre-existing data and are useful for rapidly screening the physicochemical space of a material, which is astronomically large. However, ML models are inherently interpolative, and their efficacy for searching candidates outside a material's known range of property is unresolved. Moreover, the performance of an ML model is intricately connected to its learning strategy and the volume of training data. Here, we determine the relationship between the extrapolation ability of an ML model, the size and range of its training dataset, and its learning approach. We focus on a canonical problem of predicting the properties of a copolymer as a function of the sequence of its monomers. Tree search algorithms, which learn the similarity between polymer structures, are found to be inefficient for extrapolation. Conversely, the extrapolation capability of neural networks and XGBoost models, which attempt to learn the underlying functional correlation between the structure and property of polymers, show strong correlations with the volume and range of training data. These findings have important implications on ML-based new material development.

When does deep learning fail and how to tackle it? A critical analysis on polymer sequence-property surrogate models

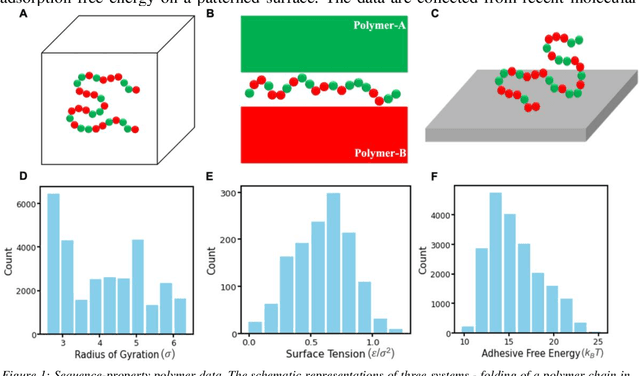
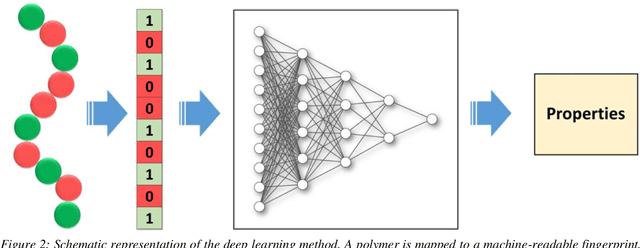
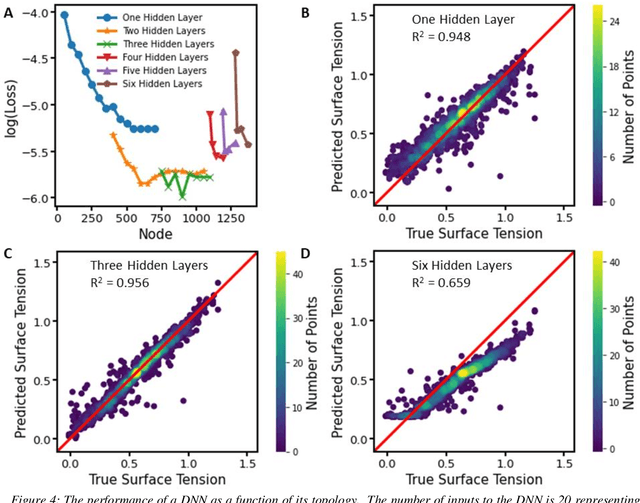
Deep learning models are gaining popularity and potency in predicting polymer properties. These models can be built using pre-existing data and are useful for the rapid prediction of polymer properties. However, the performance of a deep learning model is intricately connected to its topology and the volume of training data. There is no facile protocol available to select a deep learning architecture, and there is a lack of a large volume of homogeneous sequence-property data of polymers. These two factors are the primary bottleneck for the efficient development of deep learning models. Here we assess the severity of these factors and propose new algorithms to address them. We show that a linear layer-by-layer expansion of a neural network can help in identifying the best neural network topology for a given problem. Moreover, we map the discrete sequence space of a polymer to a continuous one-dimensional latent space using a machine learning pipeline to identify minimal data points for building a universal deep learning model. We implement these approaches for three representative cases of building sequence-property surrogate models, viz., the single-molecule radius of gyration of a copolymer, adhesive free energy of a copolymer, and copolymer compatibilizer, demonstrating the generality of the proposed strategies. This work establishes efficient methods for building universal deep learning models with minimal data and hyperparameters for predicting sequence-defined properties of polymers.