Goal-oriented inference of environment from redundant observations

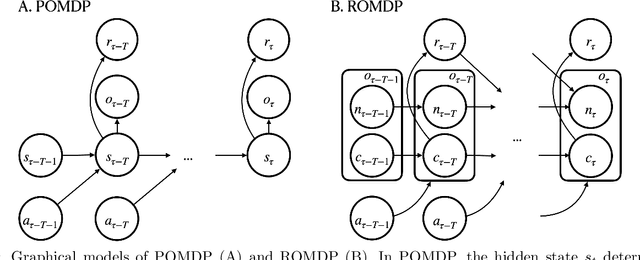
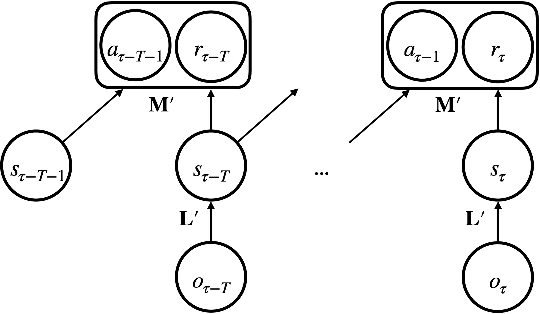
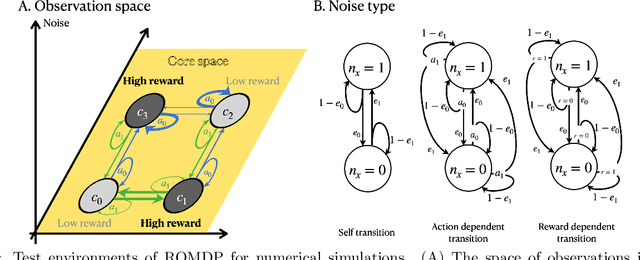
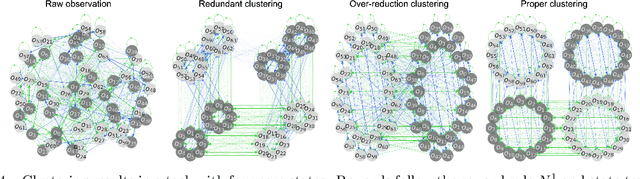
The agent learns to organize decision behavior to achieve a behavioral goal, such as reward maximization, and reinforcement learning is often used for this optimization. Learning an optimal behavioral strategy is difficult under the uncertainty that events necessary for learning are only partially observable, called as Partially Observable Markov Decision Process (POMDP). However, the real-world environment also gives many events irrelevant to reward delivery and an optimal behavioral strategy. The conventional methods in POMDP, which attempt to infer transition rules among the entire observations, including irrelevant states, are ineffective in such an environment. Supposing Redundantly Observable Markov Decision Process (ROMDP), here we propose a method for goal-oriented reinforcement learning to efficiently learn state transition rules among reward-related "core states'' from redundant observations. Starting with a small number of initial core states, our model gradually adds new core states to the transition diagram until it achieves an optimal behavioral strategy consistent with the Bellman equation. We demonstrate that the resultant inference model outperforms the conventional method for POMDP. We emphasize that our model only containing the core states has high explainability. Furthermore, the proposed method suits online learning as it suppresses memory consumption and improves learning speed.

Clustering of non-Gaussian data by variational Bayes for normal inverse Gaussian mixture models

Finite mixture models, typically Gaussian mixtures, are well known and widely used as model-based clustering. In practical situations, there are many non-Gaussian data that are heavy-tailed and/or asymmetric. Normal inverse Gaussian (NIG) distributions are normal-variance mean which mixing densities are inverse Gaussian distributions and can be used for both haavy-tail and asymmetry. For NIG mixture models, both expectation-maximization method and variational Bayesian (VB) algorithms have been proposed. However, the existing VB algorithm for NIG mixture have a disadvantage that the shape of the mixing density is limited. In this paper, we propose another VB algorithm for NIG mixture that improves on the shortcomings. We also propose an extension of Dirichlet process mixture models to overcome the difficulty in determining the number of clusters in finite mixture models. We evaluated the performance with artificial data and found that it outperformed Gaussian mixtures and existing implementations for NIG mixtures, especially for highly non-normative data.