Asynchronous Batch Bayesian Optimization with Pipelining Evaluations for Experimental Resource$\unicode{x2013}$constrained Conditions

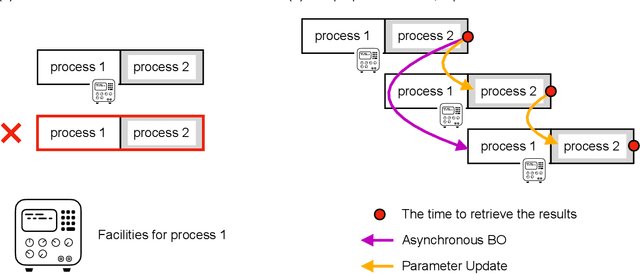
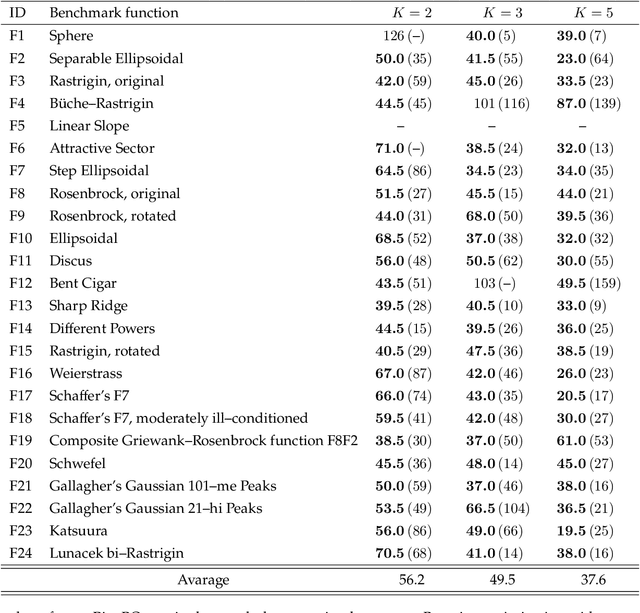
Bayesian optimization is efficient even with a small amount of data and is used in engineering and in science, including biology and chemistry. In Bayesian optimization, a parameterized model with an uncertainty is fitted to explain the experimental data, and then the model suggests parameters that would most likely improve the results. Batch Bayesian optimization reduces the processing time of optimization by parallelizing experiments. However, batch Bayesian optimization cannot be applied if the number of parallelized experiments is limited by the cost or scarcity of equipment; in such cases, sequential methods require an unrealistic amount of time. In this study, we developed pipelining Bayesian optimization (PipeBO) to reduce the processing time of optimization even with a limited number of parallel experiments. PipeBO was inspired by the pipelining of central processing unit architecture, which divides computational tasks into multiple processes. PipeBO was designed to achieve experiment parallelization by overlapping various processes of the experiments. PipeBO uses the results of completed experiments to update the parameters of running parallelized experiments. Using the Black-Box Optimization Benchmarking, which consists of 24 benchmark functions, we compared PipeBO with the sequential Bayesian optimization methods. PipeBO reduced the average processing time of optimization to about 56% for the experiments that consisted of two processes or even less for those with more processes for 20 out of the 24 functions. Overall, PipeBO parallelizes Bayesian optimization in the resource-constrained settings so that efficient optimization can be achieved.

Symbolic integration by integrating learning models with different strengths and weaknesses

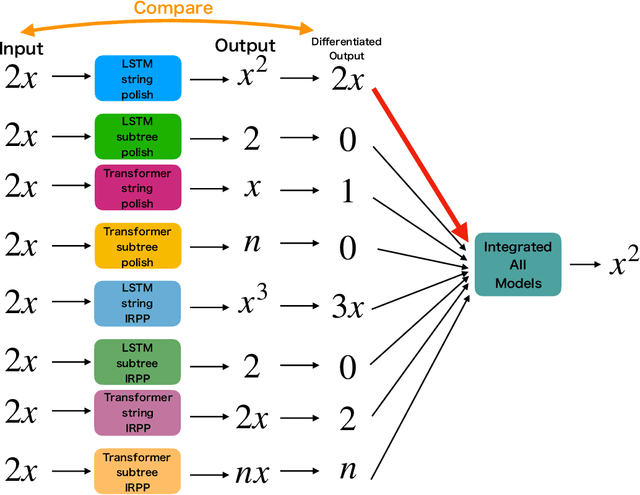
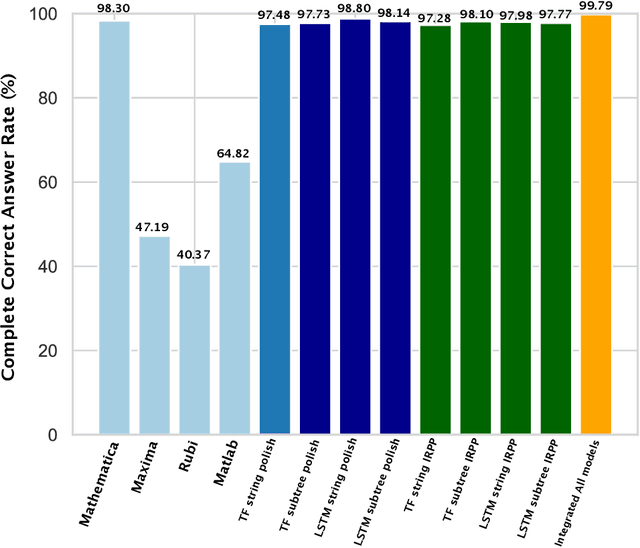
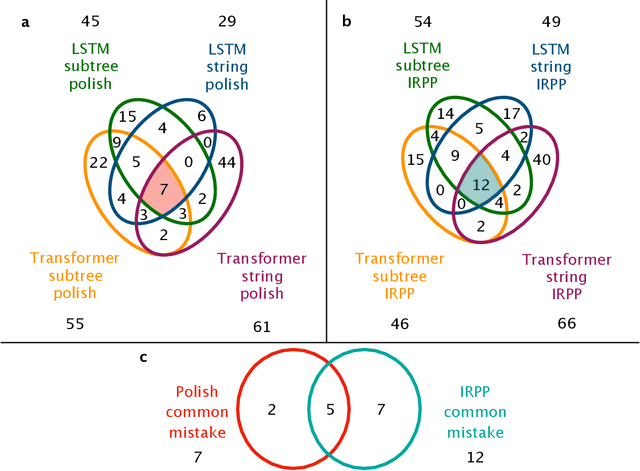
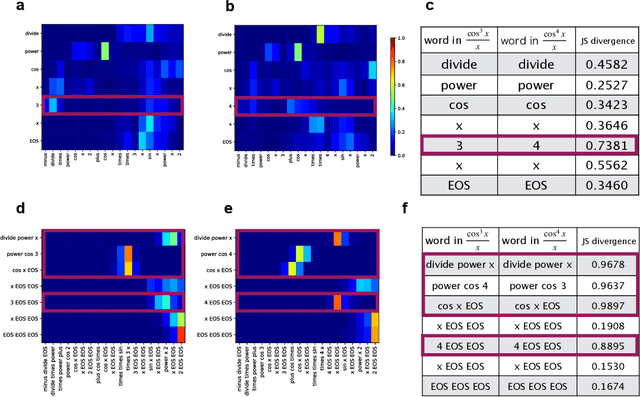
Integration is indispensable, not only in mathematics, but also in a wide range of other fields. A deep learning method has recently been developed and shown to be capable of integrating mathematical functions that could not previously be integrated on a computer. However, that method treats integration as equivalent to natural language translation and does not reflect mathematical information. In this study, we adjusted the learning model to take mathematical information into account and developed a wide range of learning models that learn the order of numerical operations more robustly. In this way, we achieved a 98.80% correct answer rate with symbolic integration, a higher rate than that of any existing method. We judged the correctness of the integration based on whether the derivative of the primitive function was consistent with the integrand. By building an integrated model based on this strategy, we achieved a 99.79% rate of correct answers with symbolic integration.