Co-clustering for directed graphs: the Stochastic co-Blockmodel and spectral algorithm Di-Sim

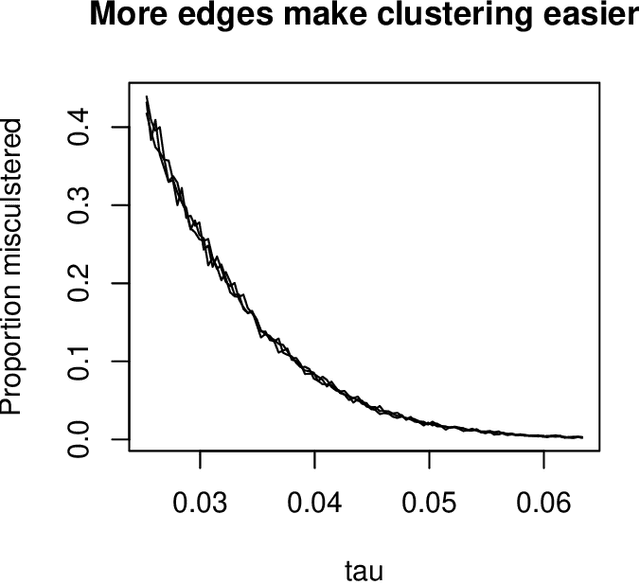
Directed graphs have asymmetric connections, yet the current graph clustering methodologies cannot identify the potentially global structure of these asymmetries. We give a spectral algorithm called di-sim that builds on a dual measure of similarity that correspond to how a node (i) sends and (ii) receives edges. Using di-sim, we analyze the global asymmetries in the networks of Enron emails, political blogs, and the c elegans neural connectome. In each example, a small subset of nodes have persistent asymmetries; these nodes send edges with one cluster, but receive edges with another cluster. Previous approaches would have assigned these asymmetric nodes to only one cluster, failing to identify their sending/receiving asymmetries. Regularization and "projection" are two steps of di-sim that are essential for spectral clustering algorithms to work in practice. The theoretical results show that these steps make the algorithm weakly consistent under the degree corrected Stochastic co-Blockmodel, a model that generalizes the Stochastic Blockmodel to allow for both (i) degree heterogeneity and (ii) the global asymmetries that we intend to detect. The theoretical results make no assumptions on the smallest degree nodes. Instead, the theorem requires that the average degree grows sufficiently fast and that the weak consistency only applies to the subset of the nodes with sufficiently large leverage scores. The results results also apply to bipartite graphs.

Regularized Spectral Clustering under the Degree-Corrected Stochastic Blockmodel

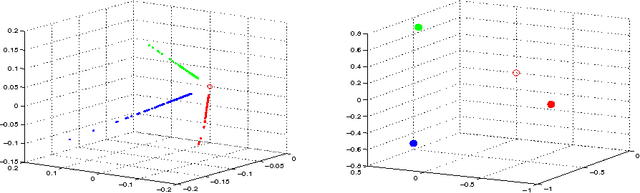
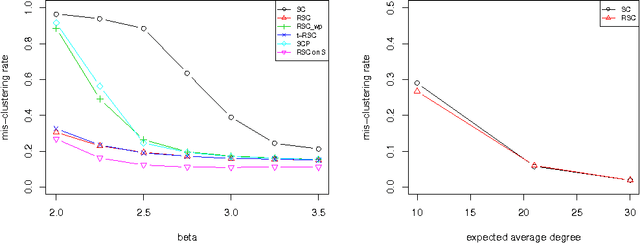
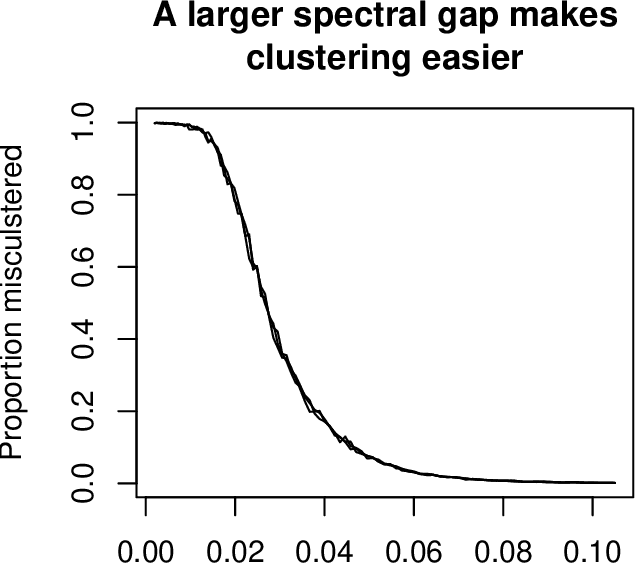
Spectral clustering is a fast and popular algorithm for finding clusters in networks. Recently, Chaudhuri et al. (2012) and Amini et al.(2012) proposed inspired variations on the algorithm that artificially inflate the node degrees for improved statistical performance. The current paper extends the previous statistical estimation results to the more canonical spectral clustering algorithm in a way that removes any assumption on the minimum degree and provides guidance on the choice of the tuning parameter. Moreover, our results show how the "star shape" in the eigenvectors--a common feature of empirical networks--can be explained by the Degree-Corrected Stochastic Blockmodel and the Extended Planted Partition model, two statistical models that allow for highly heterogeneous degrees. Throughout, the paper characterizes and justifies several of the variations of the spectral clustering algorithm in terms of these models.

The blessing of transitivity in sparse and stochastic networks

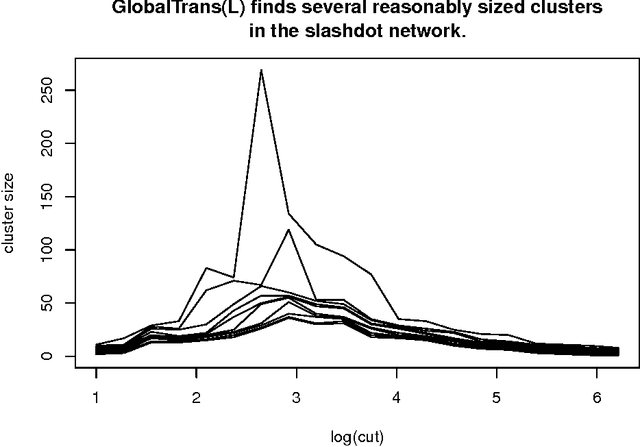
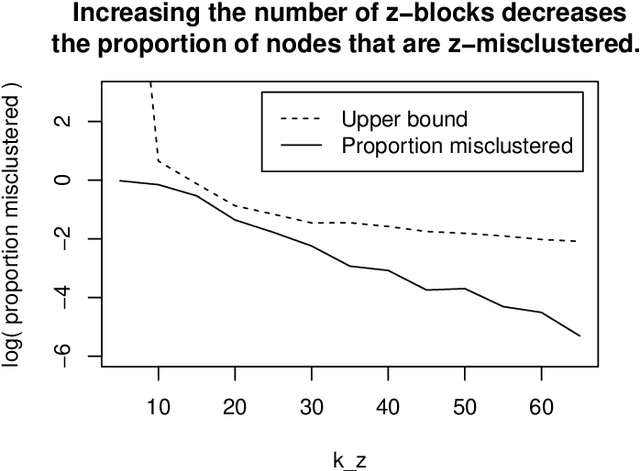
The interaction between transitivity and sparsity, two common features in empirical networks, implies that there are local regions of large sparse networks that are dense. We call this the blessing of transitivity and it has consequences for both modeling and inference. Extant research suggests that statistical inference for the Stochastic Blockmodel is more difficult when the edges are sparse. However, this conclusion is confounded by the fact that the asymptotic limit in all of the previous studies is not merely sparse, but also non-transitive. To retain transitivity, the blocks cannot grow faster than the expected degree. Thus, in sparse models, the blocks must remain asymptotically small. \n Previous algorithmic research demonstrates that small "local" clusters are more amenable to computation, visualization, and interpretation when compared to "global" graph partitions. This paper provides the first statistical results that demonstrate how these small transitive clusters are also more amenable to statistical estimation. Theorem 2 shows that a "local" clustering algorithm can, with high probability, detect a transitive stochastic block of a fixed size (e.g. 30 nodes) embedded in a large graph. The only constraint on the ambient graph is that it is large and sparse--it could be generated at random or by an adversary--suggesting a theoretical explanation for the robust empirical performance of local clustering algorithms.