Sydney Rebecca Charitos
Geometrical Postural Optimisation of 7-DoF Limb-Like Manipulators
Jul 06, 2021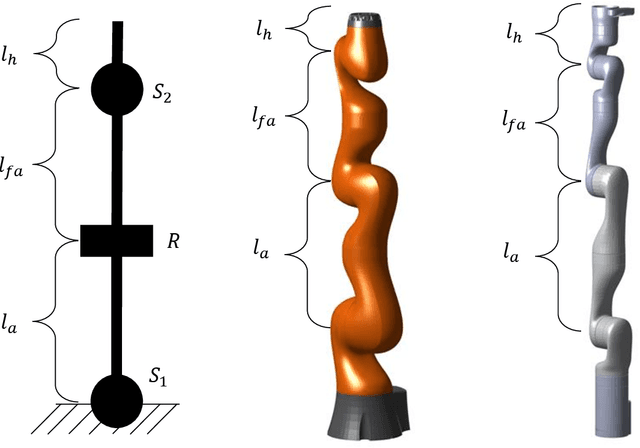
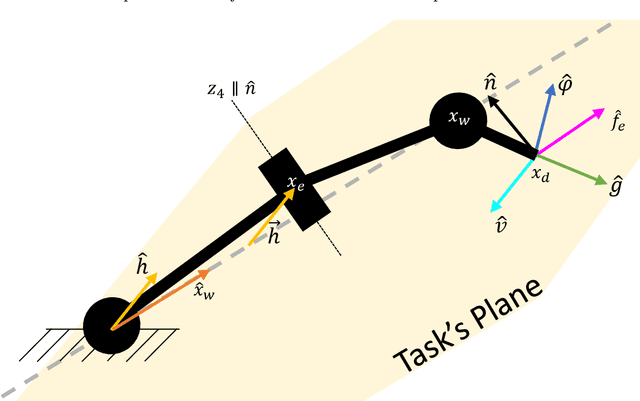
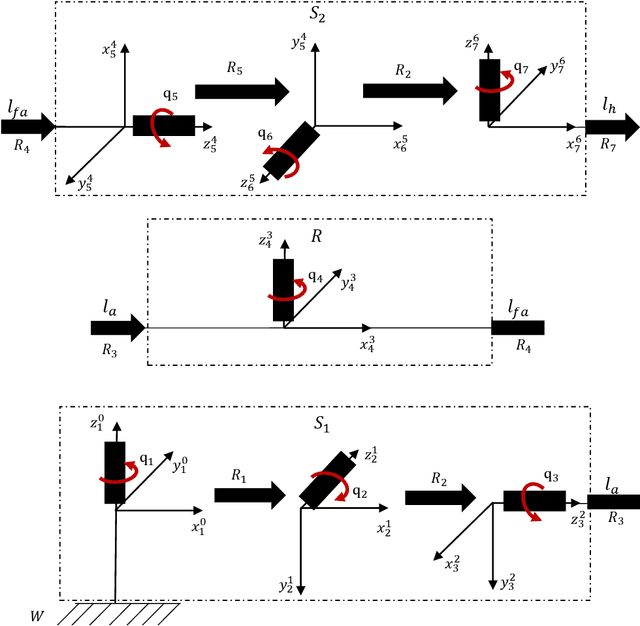
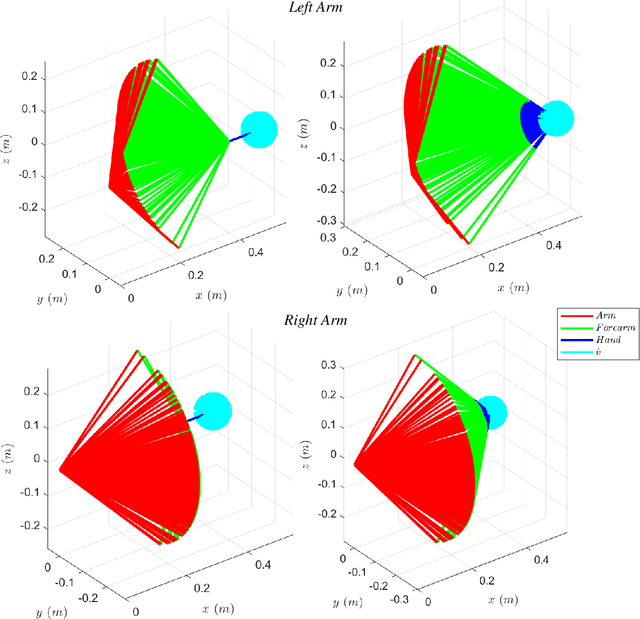
Abstract:Robots are moving towards applications in less structured environments, but their model-based controllers are challenged by the tasks' complexity and intrinsic environmental unpredictability. Studying biological motor control can provide insights into overcoming these limitations due to the high dexterity and stability observable in humans and animals. This work presents a geometrical solution to the postural optimisation of 7-DoF limbs-like mechanisms, which are robust to singularities and computationally efficient. The theoretical formulation identified two separate decoupled optimisation strategies. The shoulder and elbow strategy align the plane of motion with the expected plane of motion and guarantee the reachability of the end-posture. The wrist strategy ensures the end-effector orientation, which is essential to retain manipulability when nearing a singular configuration. The numerical results confirmed the theoretical observations and allowed us to identify the effect of different grasp strategies on system manipulability. The geometrical method was numerically tested in thousands of configurations proving to be both robust and accurate. The tested scenarios include left and right arm postures, singular configurations, and walking scenarios. The proposed geometrical approach can find application in developing efficient and robust interaction controllers that could be applied in computational neuroscience and robotics.
Exploiting Spherical Projections To Generate Human-Like Wrist Pointing Movements
Mar 08, 2021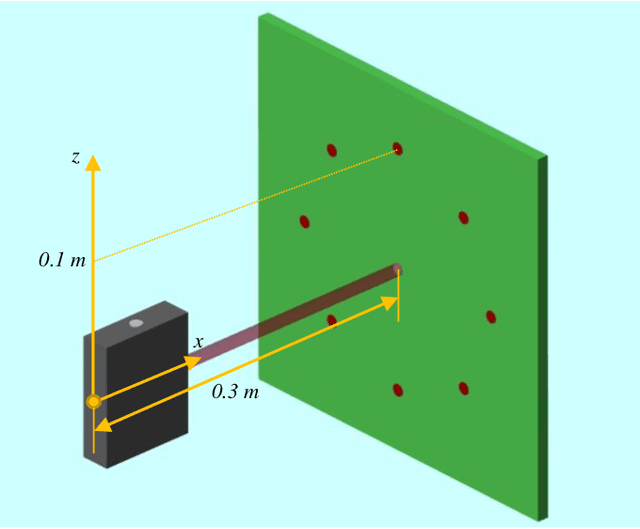
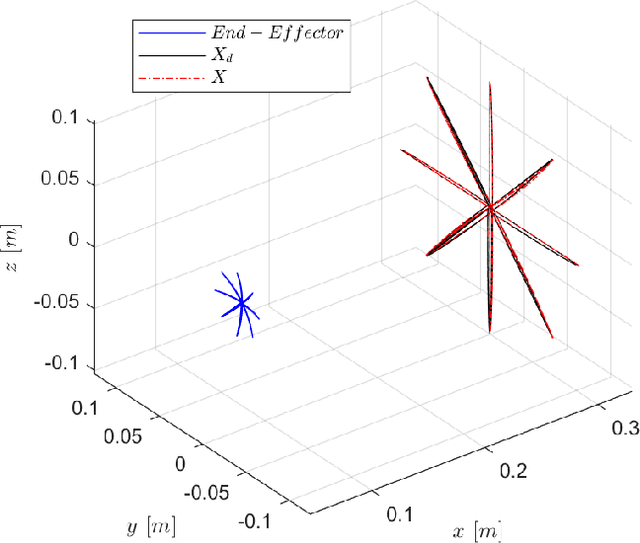
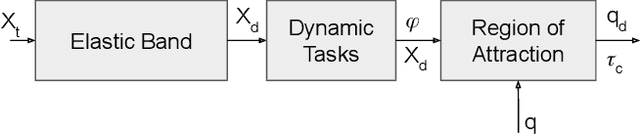
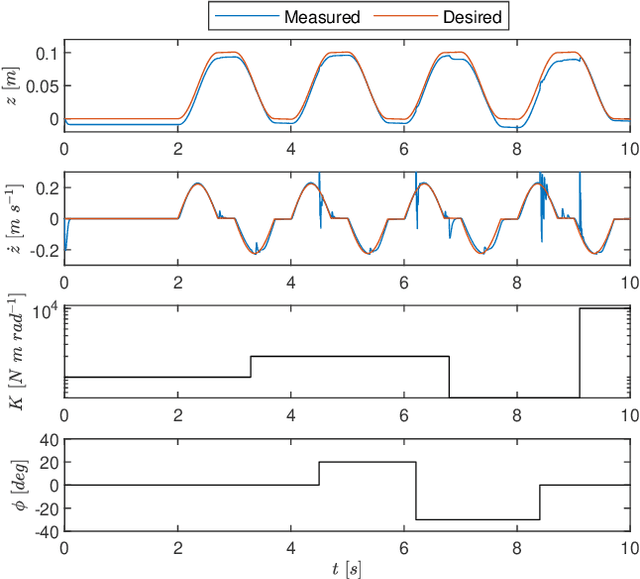
Abstract:The mechanism behind the generation of human movements is of great interest in many fields (e.g. robotics and neuroscience) to improve therapies and technologies. Optimal Feedback Control (OFC) and Passive Motion Paradigm (PMP) are currently two leading theories capable of effectively producing human-like motions, but they require solving nonlinear inverse problems to find a solution. The main benefit of using PMP is the possibility of generating path-independent movements consistent with the stereotypical behaviour observed in humans, while the equivalent OFC formulation is path-dependent. Our results demonstrate how the path-independent behaviour observed for the wrist pointing task can be explained by spherical projections of the planar tasks. The combination of the projections with the fractal impedance controller eliminates the nonlinear inverse problem, which reduces the computational cost compared to previous methodologies. The motion exploits a recently proposed PMP architecture that replaces the nonlinear inverse optimisation with a nonlinear anisotropic stiffness impedance profile generated by the Fractal Impedance Controller, reducing the computational cost and not requiring a task-dependent optimisation.
Theoretical Evidence Supporting Harmonic Reaching Trajectories
Dec 01, 2020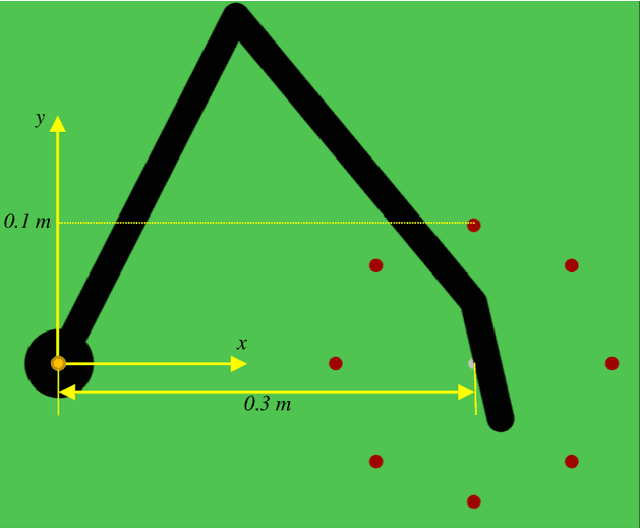

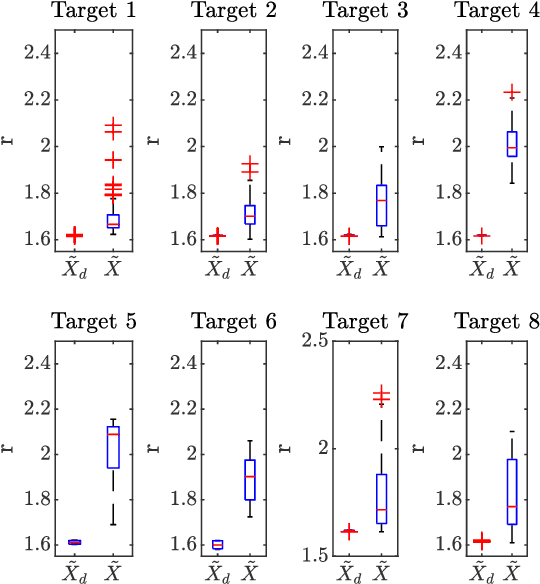
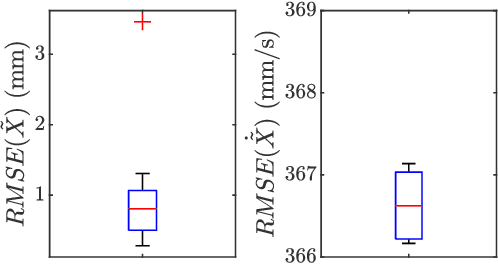
Abstract:Minimum Jerk trajectories have been long thought to be the reference trajectories for human movements due to their impressive similarity with human movements. Nevertheless, minimum jerk trajectories are not the only choice for $C^\infty$ (i.e., smooth) functions. For example, harmonic trajectories are smooth functions that can be superimposed to describe the evolution of physical systems. This paper analyses the possibility that motor control plans using harmonic trajectories, will be experimentally observed to have a minimum jerk likeness due to control signals being transported through the Central Nervous System (CNS) and muscle-skeletal system. We tested our theory on a 3-link arm simulation using a recently developed planner that we reformulated into a motor control architecture, inspired by the passive motion paradigm. The arm performed 100 movements, reaching for each target defined by the clock experiment. We analysed the shape of the trajectory planned in the CNS and executed in the physical simulator. We observed that even under ideal conditions (i.e., absence of delays and noise) the executed trajectories are similar to a minimum jerk trajectory; thus, supporting the thesis that the human brain might plan harmonic trajectories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge