Sungmin Kim
Scalable Spectral Algorithms for Community Detection in Directed Networks
Sep 23, 2013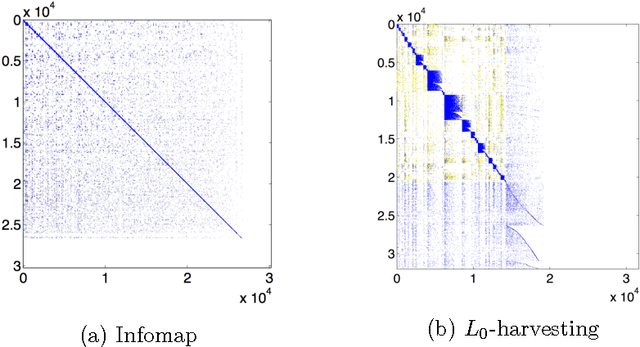

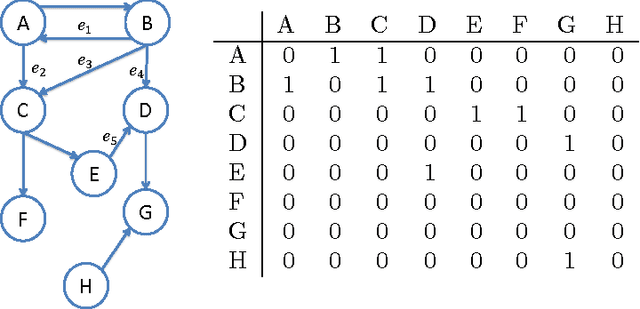

Abstract:Community detection has been one of the central problems in network studies and directed network is particularly challenging due to asymmetry among its links. In this paper, we found that incorporating the direction of links reveals new perspectives on communities regarding to two different roles, source and terminal, that a node plays in each community. Intriguingly, such communities appear to be connected with unique spectral property of the graph Laplacian of the adjacency matrix and we exploit this connection by using regularized SVD methods. We propose harvesting algorithms, coupled with regularized SVDs, that are linearly scalable for efficient identification of communities in huge directed networks. The proposed algorithm shows great performance and scalability on benchmark networks in simulations and successfully recovers communities in real network applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge