Sumitra. S
Neighborhood Preserving Kernels for Attributed Graphs
Oct 13, 2020
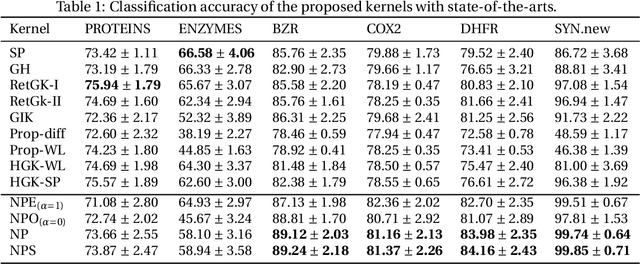
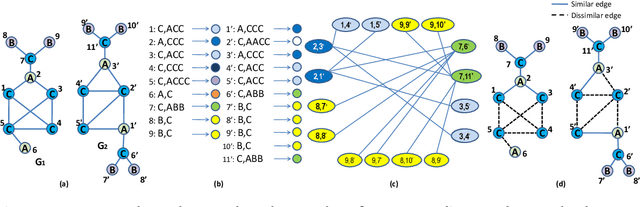
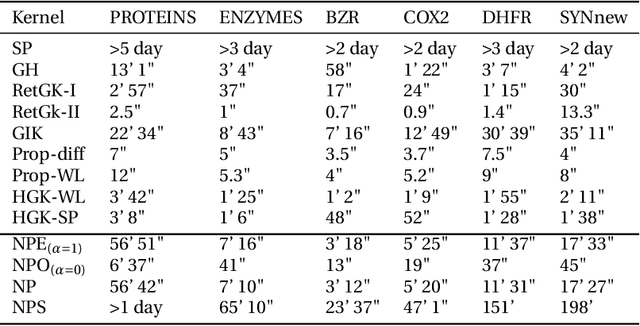
Abstract:We describe the design of a reproducing kernel suitable for attributed graphs, in which the similarity between the two graphs is defined based on the neighborhood information of the graph nodes with the aid of a product graph formulation. We represent the proposed kernel as the weighted sum of two other kernels of which one is an R-convolution kernel that processes the attribute information of the graph and the other is an optimal assignment kernel that processes label information. They are formulated in such a way that the edges processed as part of the kernel computation have the same neighborhood properties and hence the kernel proposed makes a well-defined correspondence between regions processed in graphs. These concepts are also extended to the case of the shortest paths. We identified the state-of-the-art kernels that can be mapped to such a neighborhood preserving framework. We found that the kernel value of the argument graphs in each iteration of the Weisfeiler-Lehman color refinement algorithm can be obtained recursively from the product graph formulated in our method. By incorporating the proposed kernel on support vector machines we analyzed the real-world data sets and it has shown superior performance in comparison with that of the other state-of-the-art graph kernels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge