Leveraging priors on distribution functions for multi-arm bandits

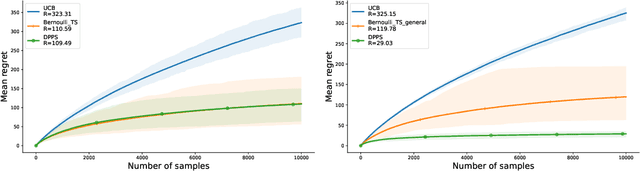
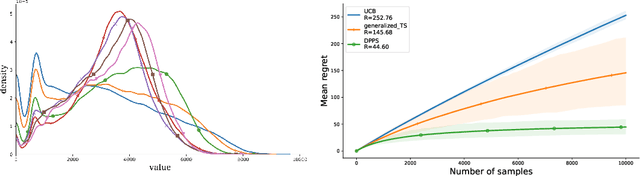
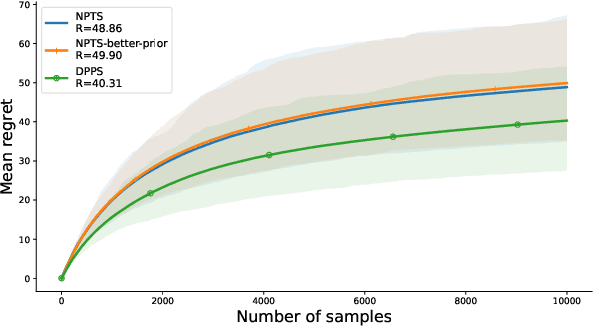
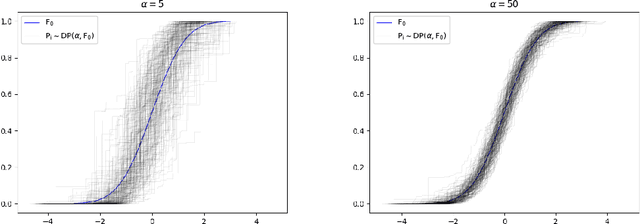
We introduce Dirichlet Process Posterior Sampling (DPPS), a Bayesian non-parametric algorithm for multi-arm bandits based on Dirichlet Process (DP) priors. Like Thompson-sampling, DPPS is a probability-matching algorithm, i.e., it plays an arm based on its posterior-probability of being optimal. Instead of assuming a parametric class for the reward generating distribution of each arm, and then putting a prior on the parameters, in DPPS the reward generating distribution is directly modeled using DP priors. DPPS provides a principled approach to incorporate prior belief about the bandit environment, and in the noninformative limit of the DP posteriors (i.e. Bayesian Bootstrap), we recover Non Parametric Thompson Sampling (NPTS), a popular non-parametric bandit algorithm, as a special case of DPPS. We employ stick-breaking representation of the DP priors, and show excellent empirical performance of DPPS in challenging synthetic and real world bandit environments. Finally, using an information-theoretic analysis, we show non-asymptotic optimality of DPPS in the Bayesian regret setup.

Restoring Chaos Using Deep Reinforcement Learning

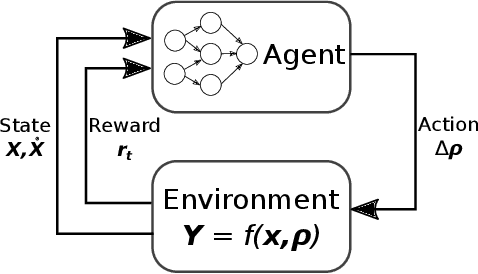
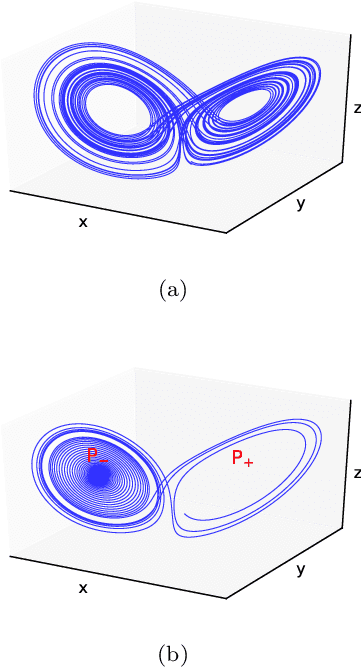
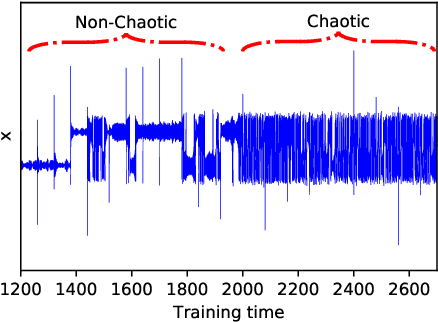
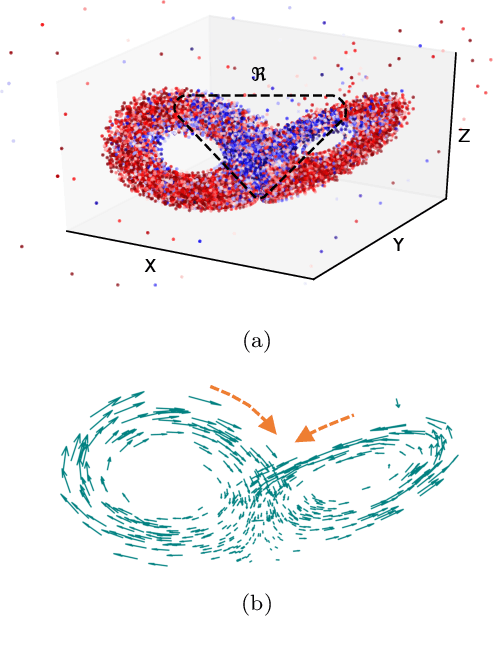
A catastrophic bifurcation in non-linear dynamical systems, called crisis, often leads to their convergence to an undesirable non-chaotic state after some initial chaotic transients. Preventing such behavior has proved to be quite challenging. We demonstrate that deep Reinforcement Learning (RL) is able to restore chaos in a transiently-chaotic regime of the Lorenz system of equations. Without requiring any a priori knowledge of the underlying dynamics of the governing equations, the RL agent discovers an effective perturbation strategy for sustaining the chaotic trajectory. We analyze the agent's autonomous control-decisions, and identify and implement a simple control-law that successfully restores chaos in the Lorenz system. Our results demonstrate the utility of using deep RL for controlling the occurrence of catastrophes and extreme-events in non-linear dynamical systems.