Restoring Chaos Using Deep Reinforcement Learning
Paper and Code
Nov 27, 2019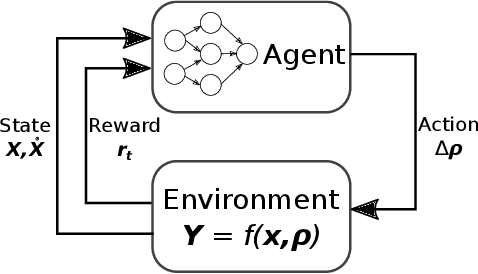
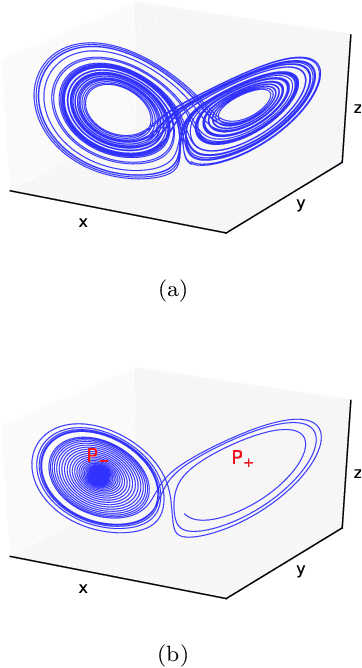
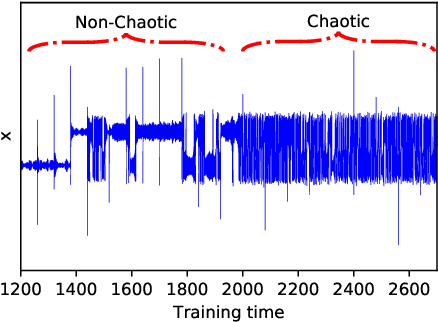
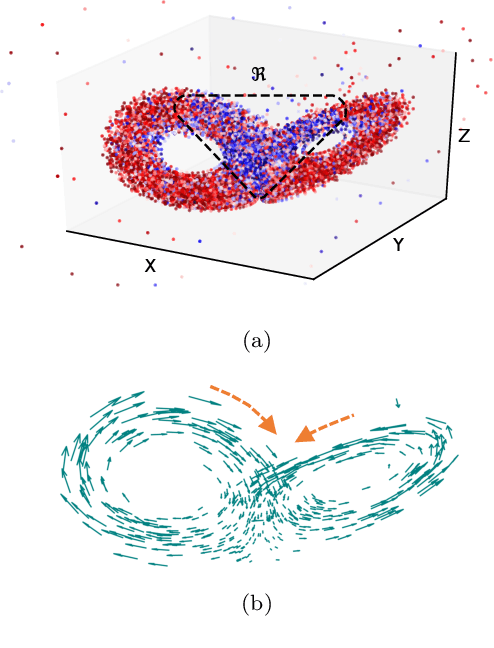
A catastrophic bifurcation in non-linear dynamical systems, called crisis, often leads to their convergence to an undesirable non-chaotic state after some initial chaotic transients. Preventing such behavior has proved to be quite challenging. We demonstrate that deep Reinforcement Learning (RL) is able to restore chaos in a transiently-chaotic regime of the Lorenz system of equations. Without requiring any a priori knowledge of the underlying dynamics of the governing equations, the RL agent discovers an effective perturbation strategy for sustaining the chaotic trajectory. We analyze the agent's autonomous control-decisions, and identify and implement a simple control-law that successfully restores chaos in the Lorenz system. Our results demonstrate the utility of using deep RL for controlling the occurrence of catastrophes and extreme-events in non-linear dynamical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge