A convergent scheme for the Bayesian filtering problem based on the Fokker--Planck equation and deep splitting

A numerical scheme for approximating the nonlinear filtering density is introduced and its convergence rate is established, theoretically under a parabolic H\"{o}rmander condition, and empirically for two examples. For the prediction step, between the noisy and partial measurements at discrete times, the scheme approximates the Fokker--Planck equation with a deep splitting scheme, and performs an exact update through Bayes' formula. This results in a classical prediction-update filtering algorithm that operates online for new observation sequences post-training. The algorithm employs a sampling-based Feynman--Kac approach, designed to mitigate the curse of dimensionality. Our convergence proof relies on the Malliavin integration-by-parts formula. As a corollary we obtain the convergence rate for the approximation of the Fokker--Planck equation alone, disconnected from the filtering problem.

An energy-based deep splitting method for the nonlinear filtering problem

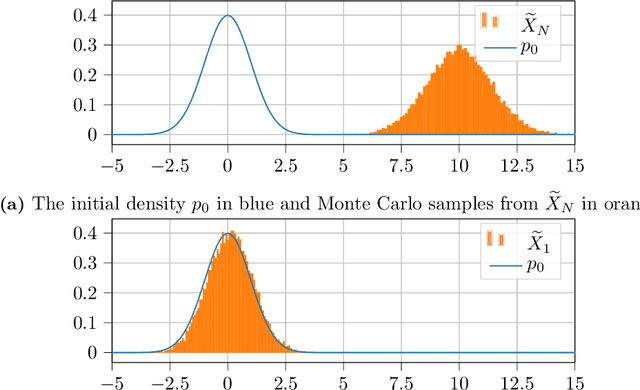
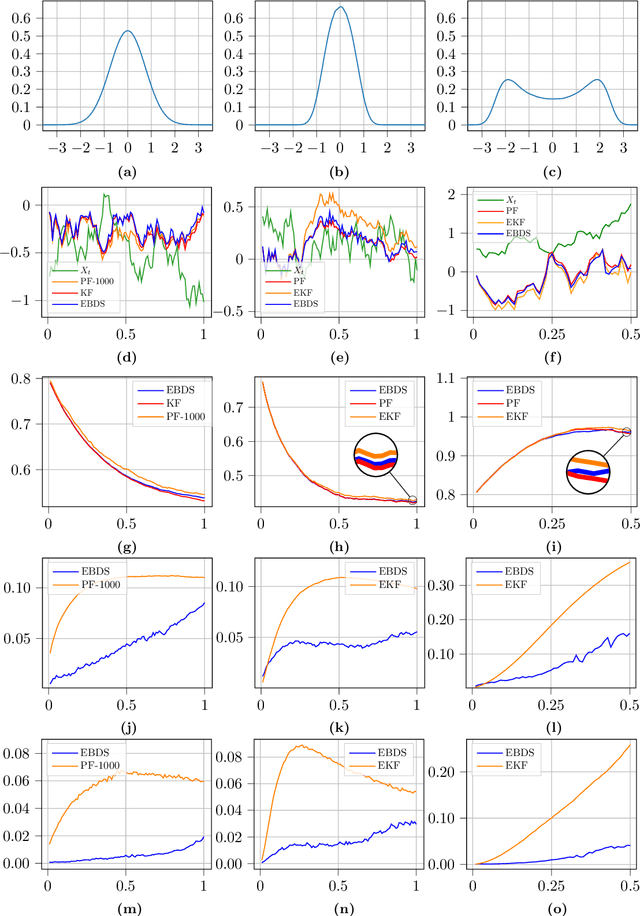
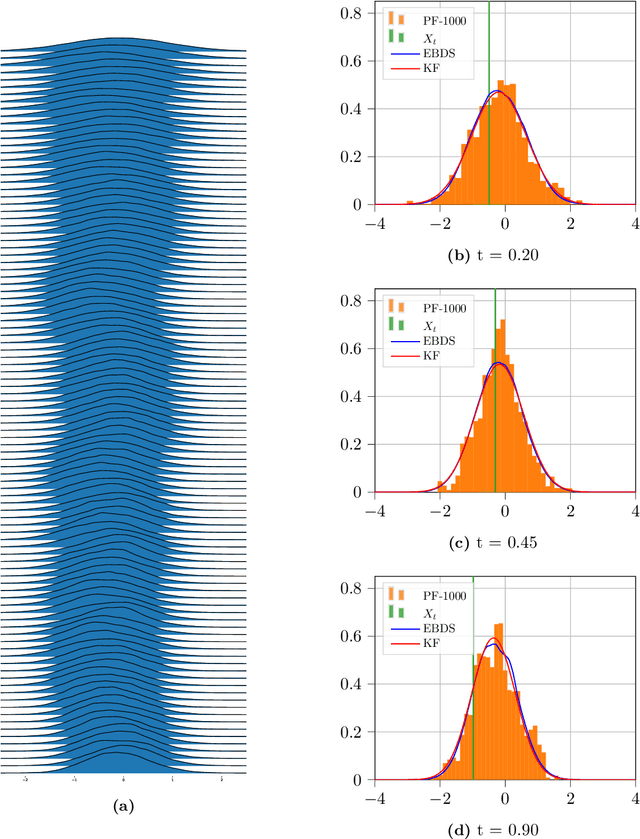
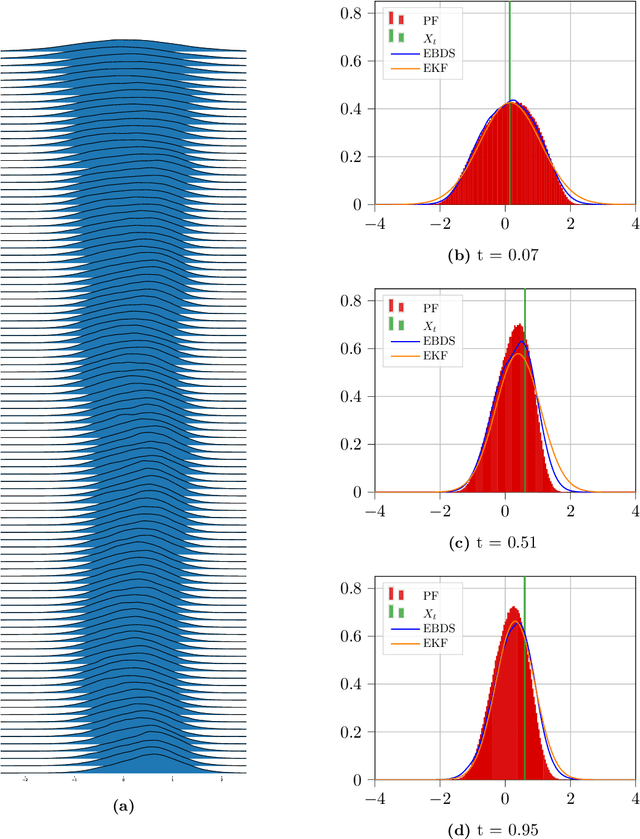
The purpose of this paper is to explore the use of deep learning for the solution of the nonlinear filtering problem. This is achieved by solving the Zakai equation by a deep splitting method, previously developed for approximate solution of (stochastic) partial differential equations. This is combined with an energy-based model for the approximation of functions by a deep neural network. This results in a computationally fast filter that takes observations as input and that does not require re-training when new observations are received. The method is tested on three examples, one linear Gaussian and two nonlinear. The method shows promising performance when benchmarked against the Kalman filter and the bootstrap particle filter.