Hidden Markov Models with mixtures as emission distributions

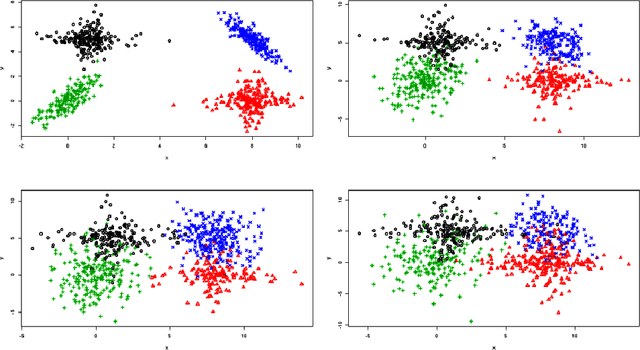
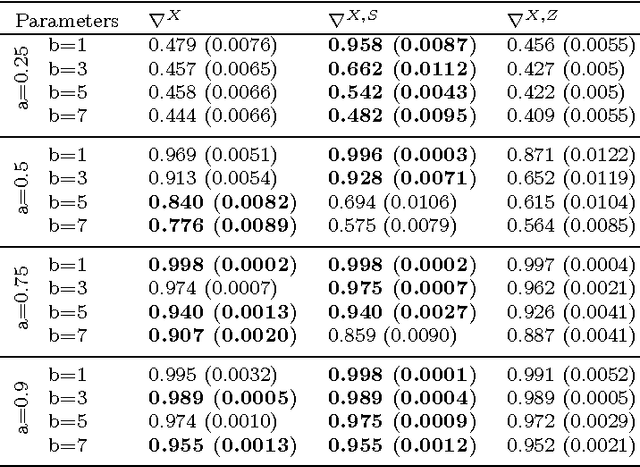
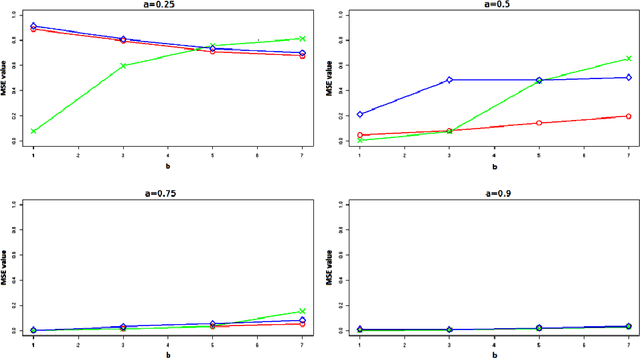
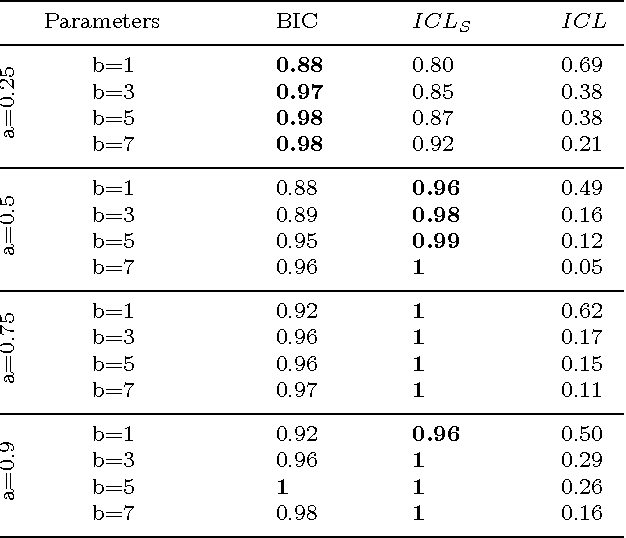
In unsupervised classification, Hidden Markov Models (HMM) are used to account for a neighborhood structure between observations. The emission distributions are often supposed to belong to some parametric family. In this paper, a semiparametric modeling where the emission distributions are a mixture of parametric distributions is proposed to get a higher flexibility. We show that the classical EM algorithm can be adapted to infer the model parameters. For the initialisation step, starting from a large number of components, a hierarchical method to combine them into the hidden states is proposed. Three likelihood-based criteria to select the components to be combined are discussed. To estimate the number of hidden states, BIC-like criteria are derived. A simulation study is carried out both to determine the best combination between the merging criteria and the model selection criteria and to evaluate the accuracy of classification. The proposed method is also illustrated using a biological dataset from the model plant Arabidopsis thaliana. A R package HMMmix is freely available on the CRAN.

Variational Bayes approach for model aggregation in unsupervised classification with Markovian dependency

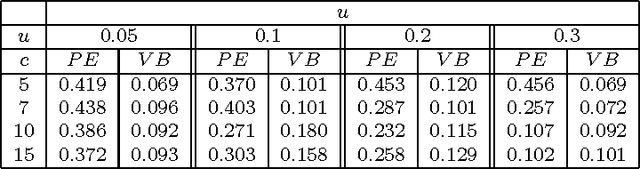
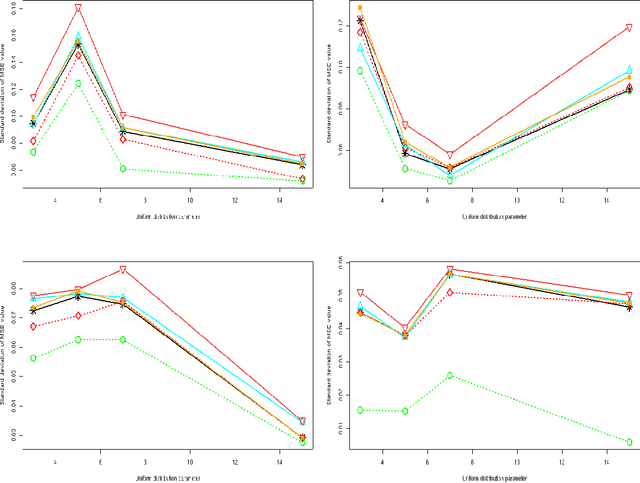
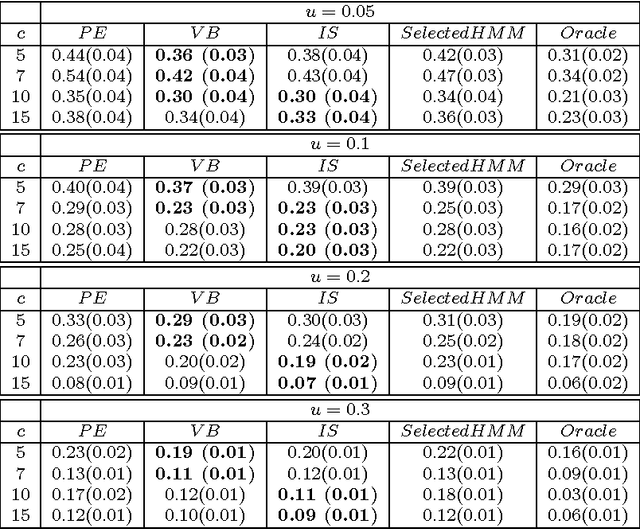
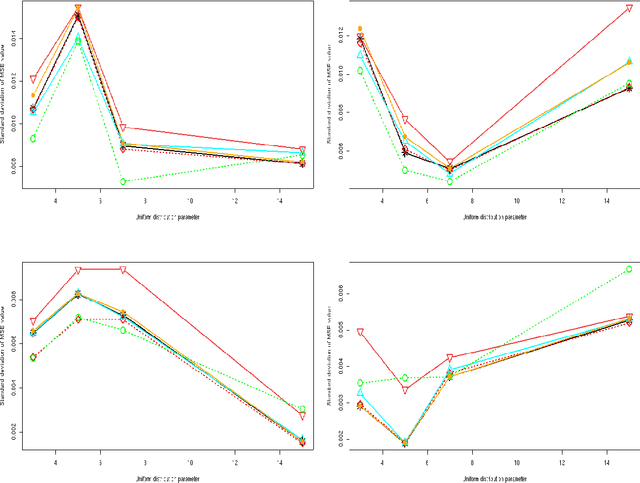
We consider a binary unsupervised classification problem where each observation is associated with an unobserved label that we want to retrieve. More precisely, we assume that there are two groups of observation: normal and abnormal. The `normal' observations are coming from a known distribution whereas the distribution of the `abnormal' observations is unknown. Several models have been developed to fit this unknown distribution. In this paper, we propose an alternative based on a mixture of Gaussian distributions. The inference is done within a variational Bayesian framework and our aim is to infer the posterior probability of belonging to the class of interest. To this end, it makes no sense to estimate the mixture component number since each mixture model provides more or less relevant information to the posterior probability estimation. By computing a weighted average (named aggregated estimator) over the model collection, Bayesian Model Averaging (BMA) is one way of combining models in order to account for information provided by each model. The aim is then the estimation of the weights and the posterior probability for one specific model. In this work, we derive optimal approximations of these quantities from the variational theory and propose other approximations of the weights. To perform our method, we consider that the data are dependent (Markovian dependency) and hence we consider a Hidden Markov Model. A simulation study is carried out to evaluate the accuracy of the estimates in terms of classification. We also present an application to the analysis of public health surveillance systems.