The effect of variable labels on deep learning models trained to predict breast density

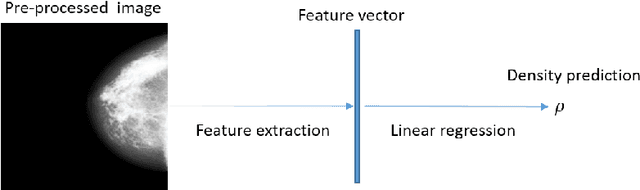
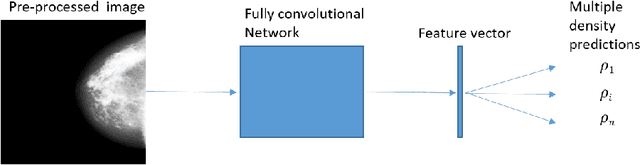
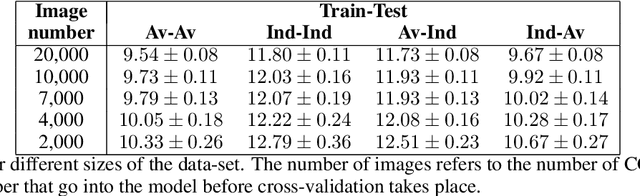
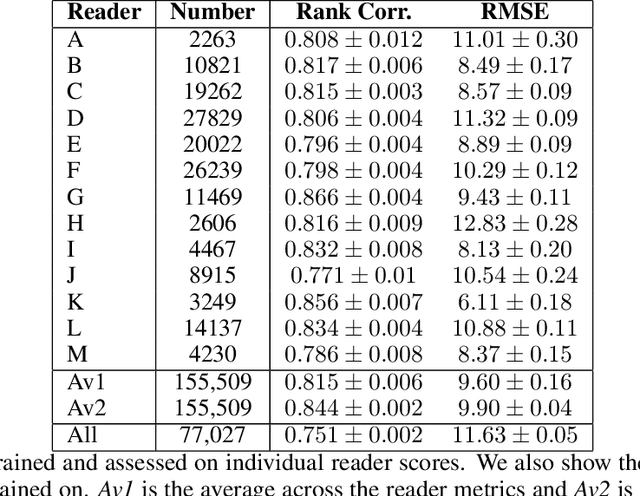
Purpose: High breast density is associated with reduced efficacy of mammographic screening and increased risk of developing breast cancer. Accurate and reliable automated density estimates can be used for direct risk prediction and passing density related information to further predictive models. Expert reader assessments of density show a strong relationship to cancer risk but also inter-reader variation. The effect of label variability on model performance is important when considering how to utilise automated methods for both research and clinical purposes. Methods: We utilise subsets of images with density labels to train a deep transfer learning model which is used to assess how label variability affects the mapping from representation to prediction. We then create two end-to-end deep learning models which allow us to investigate the effect of label variability on the model representation formed. Results: We show that the trained mappings from representations to labels are altered considerably by the variability of reader scores. Training on labels with distribution variation removed causes the Spearman rank correlation coefficients to rise from $0.751\pm0.002$ to either $0.815\pm0.006$ when averaging across readers or $0.844\pm0.002$ when averaging across images. However, when we train different models to investigate the representation effect we see little difference, with Spearman rank correlation coefficients of $0.846\pm0.006$ and $0.850\pm0.006$ showing no statistically significant difference in the quality of the model representation with regard to density prediction. Conclusions: We show that the mapping between representation and mammographic density prediction is significantly affected by label variability. However, the effect of the label variability on the model representation is limited.

A Variational Autoencoder for Probabilistic Non-Negative Matrix Factorisation

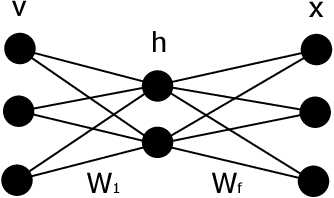
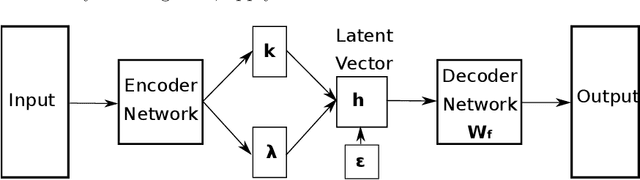
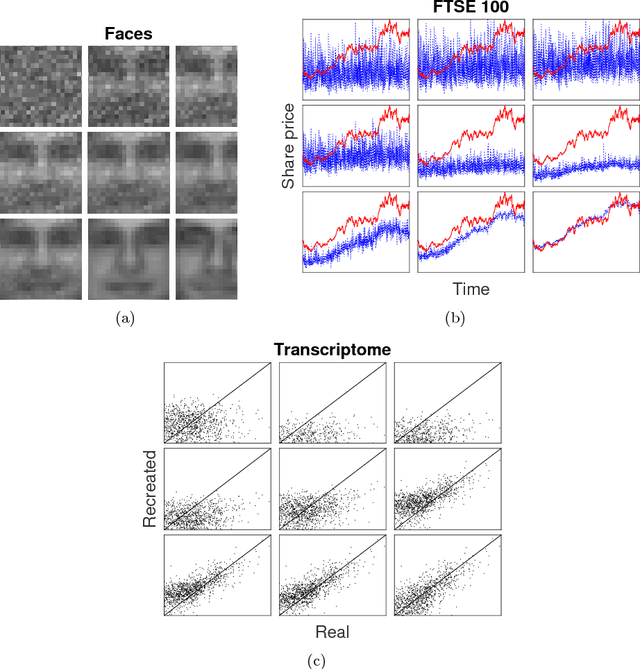
We introduce and demonstrate the variational autoencoder (VAE) for probabilistic non-negative matrix factorisation (PAE-NMF). We design a network which can perform non-negative matrix factorisation (NMF) and add in aspects of a VAE to make the coefficients of the latent space probabilistic. By restricting the weights in the final layer of the network to be non-negative and using the non-negative Weibull distribution we produce a probabilistic form of NMF which allows us to generate new data and find a probability distribution that effectively links the latent and input variables. We demonstrate the effectiveness of PAE-NMF on three heterogeneous datasets: images, financial time series and genomic.

Minimum description length as an objective function for non-negative matrix factorization

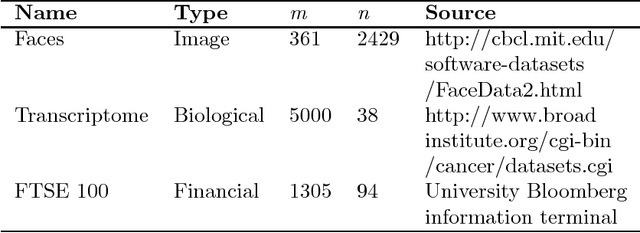
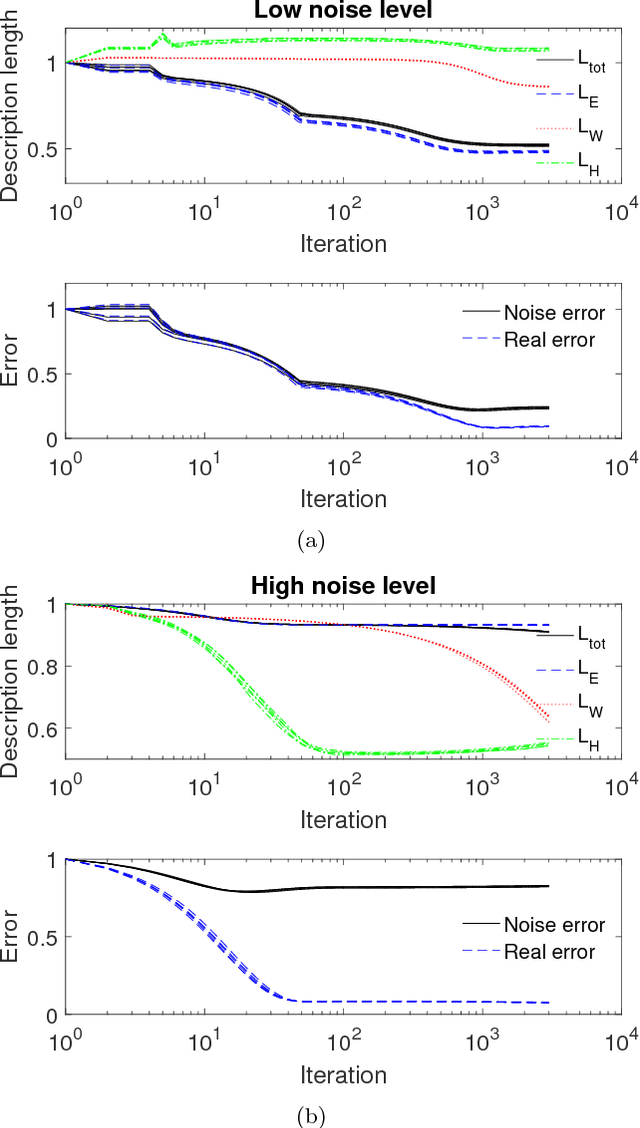
Non-negative matrix factorization (NMF) is a dimensionality reduction technique which tends to produce a sparse representation of data. Commonly, the error between the actual and recreated matrices is used as an objective function, but this method may not produce the type of representation we desire as it allows for the complexity of the model to grow, constrained only by the size of the subspace and the non-negativity requirement. If additional constraints, such as sparsity, are imposed the question of parameter selection becomes critical. Instead of adding sparsity constraints in an ad-hoc manner we propose a novel objective function created by using the principle of minimum description length (MDL). Our formulation, MDL-NMF, automatically trades off between the complexity and accuracy of the model using a principled approach with little parameter selection or the need for domain expertise. We demonstrate our model works effectively on three heterogeneous data-sets and on a range of semi-synthetic data showing the broad applicability of our method.