Steve Vott
RamseyRL: A Framework for Intelligent Ramsey Number Counterexample Searching
Aug 23, 2023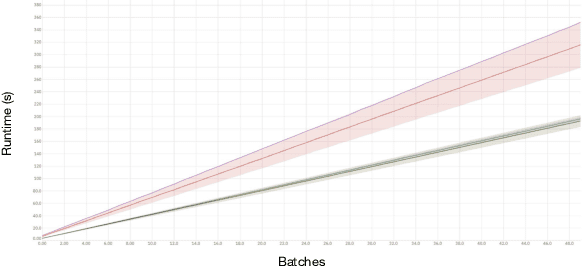
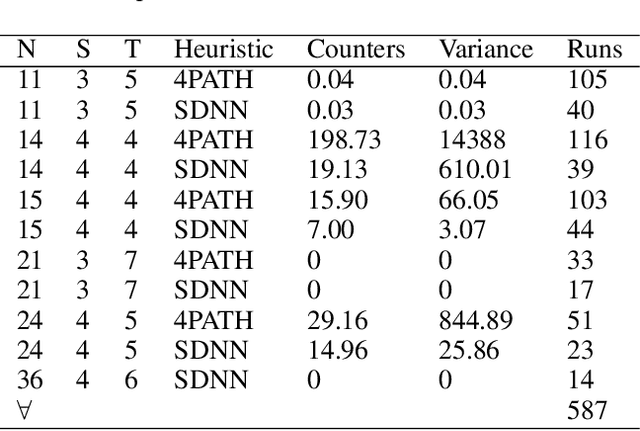
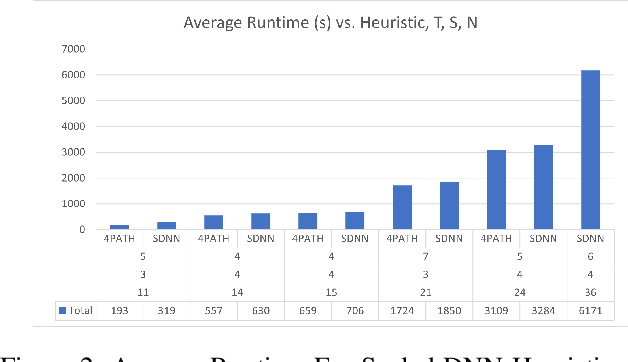
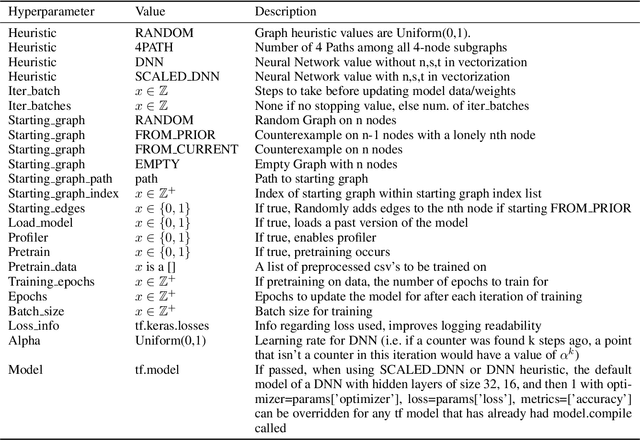
Abstract:The Ramsey number is the minimum number of nodes, $n = R(s, t)$, such that all undirected simple graphs of order $n$, contain a clique of order $s$, or an independent set of order $t$. This paper explores the application of a best first search algorithm and reinforcement learning (RL) techniques to find counterexamples to specific Ramsey numbers. We incrementally improve over prior search methods such as random search by introducing a graph vectorization and deep neural network (DNN)-based heuristic, which gauge the likelihood of a graph being a counterexample. The paper also proposes algorithmic optimizations to confine a polynomial search runtime. This paper does not aim to present new counterexamples but rather introduces and evaluates a framework supporting Ramsey counterexample exploration using other heuristics. Code and methods are made available through a PyPI package and GitHub repository.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge