Stephane Operto
Wave simulation in non-smooth media by PINN with quadratic neural network and PML condition
Aug 16, 2022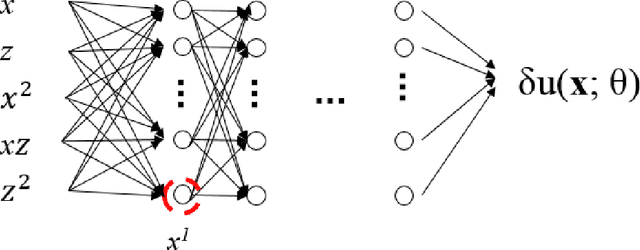



Abstract:Frequency-domain simulation of seismic waves plays an important role in seismic inversion, but it remains challenging in large models. The recently proposed physics-informed neural network (PINN), as an effective deep learning method, has achieved successful applications in solving a wide range of partial differential equations (PDEs), and there is still room for improvement on this front. For example, PINN can lead to inaccurate solutions when PDE coefficients are non-smooth and describe structurally-complex media. In this paper, we solve the acoustic and visco-acoustic scattered-field wave equation in the frequency domain with PINN instead of the wave equation to remove source singularity. We first illustrate that non-smooth velocity models lead to inaccurate wavefields when no boundary conditions are implemented in the loss function. Then, we add the perfectly matched layer (PML) conditions in the loss function of PINN and design a quadratic neural network to overcome the detrimental effects of non-smooth models in PINN. We show that PML and quadratic neurons improve the results as well as attenuation and discuss the reason for this improvement. We also illustrate that a network trained during a wavefield simulation can be used to pre-train the neural network of another wavefield simulation after PDE-coefficient alteration and improve the convergence speed accordingly. This pre-training strategy should find application in iterative full waveform inversion (FWI) and time-lag target-oriented imaging when the model perturbation between two consecutive iterations or two consecutive experiments can be small.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge