Global Vertices and the Noising Paradox

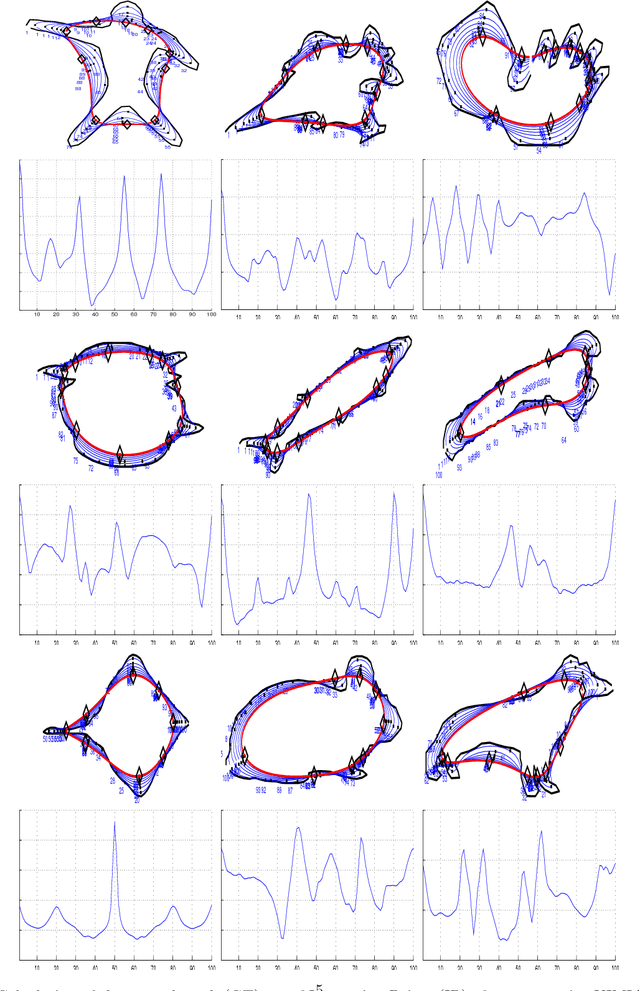
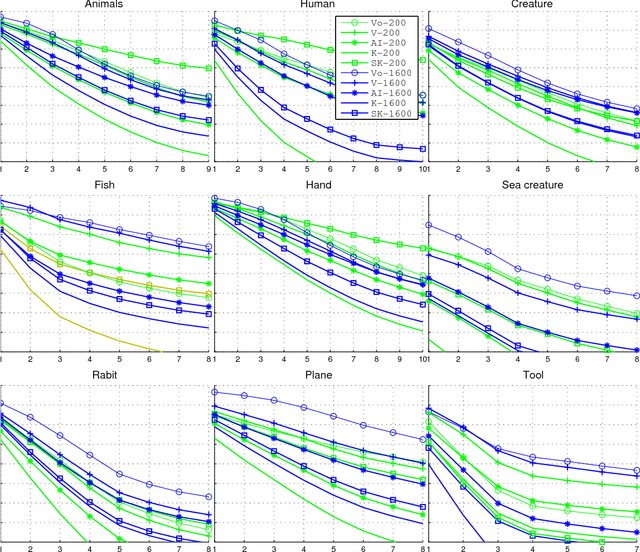
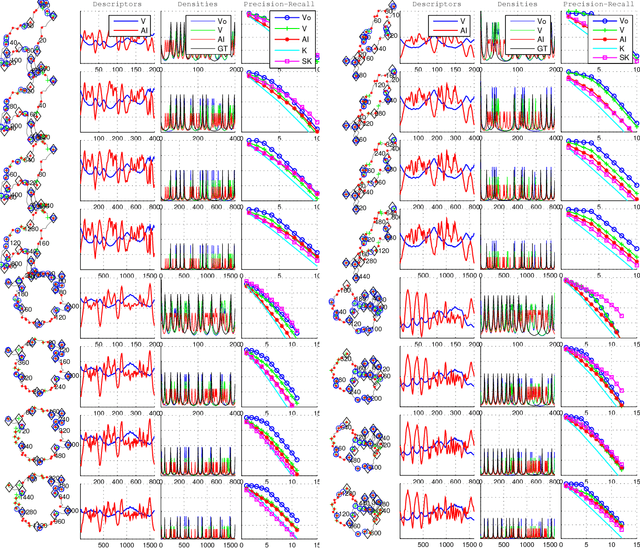
A theoretical and experimental analysis related to the identification of vertices of unknown shapes is presented. Shapes are seen as real functions of their closed boundary. Unlike traditional approaches, which see curvature as the rate of change of the tangent to the curve, an alternative global perspective of curvature is examined providing insight into the process of noise-enabled vertex localization. The analysis leads to a paradox, that certain vertices can be localized better in the presence of noise. The concept of noising is thus considered and a relevant global method for localizing "Global Vertices" is investigated. Theoretical analysis reveals that induced noise can help localizing certain vertices if combined with global descriptors. Experiments with noise and a comparison to localized methods validate the theoretical results.

Incremental Noising and its Fractal Behavior

This manuscript is about further elucidating the concept of noising. The concept of noising first appeared in \cite{CVPR14}, in the context of curvature estimation and vertex localization on planar shapes. There are indications that noising can play for global methods the role smoothing plays for local methods in this task. This manuscript is about investigating this claim by introducing incremental noising, in a recursive deterministic manner, analogous to how smoothing is extended to progressive smoothing in similar tasks. As investigating the properties and behavior of incremental noising is the purpose of this manuscript, a surprising connection between incremental noising and progressive smoothing is revealed by the experiments. To explain this phenomenon, the fractal and the space filling properties of the two methods respectively, are considered in a unifying context.