Stefano Benedettini
Boolean Networks Design by Genetic Algorithms
Jan 31, 2011
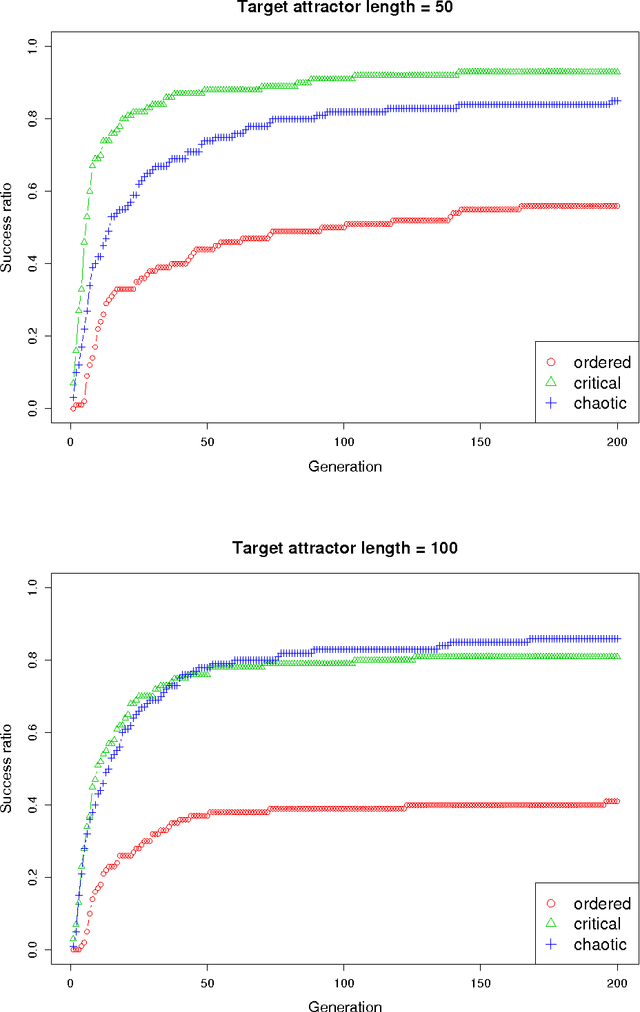


Abstract:We present and discuss the results of an experimental analysis in the design of Boolean networks by means of genetic algorithms. A population of networks is evolved with the aim of finding a network such that the attractor it reaches is of required length $l$. In general, any target can be defined, provided that it is possible to model the task as an optimisation problem over the space of networks. We experiment with different initial conditions for the networks, namely in ordered, chaotic and critical regions, and also with different target length values. Results show that all kinds of initial networks can attain the desired goal, but with different success ratios: initial populations composed of critical or chaotic networks are more likely to reach the target. Moreover, the evolution starting from critical networks achieves the best overall performance. This study is the first step toward the use of search algorithms as tools for automatically design Boolean networks with required properties.
* 13 pages, 7 figures, 2 tables
Analysis of attractor distances in Random Boolean Networks
Nov 21, 2010

Abstract:We study the properties of the distance between attractors in Random Boolean Networks, a prominent model of genetic regulatory networks. We define three distance measures, upon which attractor distance matrices are constructed and their main statistic parameters are computed. The experimental analysis shows that ordered networks have a very clustered set of attractors, while chaotic networks' attractors are scattered; critical networks show, instead, a pattern with characteristics of both ordered and chaotic networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge