Statistical analysis of Wasserstein GANs with applications to time series forecasting

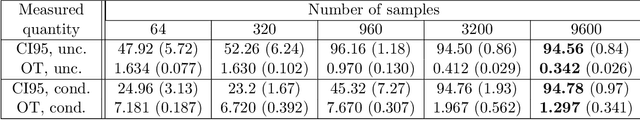
We provide statistical theory for conditional and unconditional Wasserstein generative adversarial networks (WGANs) in the framework of dependent observations. We prove upper bounds for the excess Bayes risk of the WGAN estimators with respect to a modified Wasserstein-type distance. Furthermore, we formalize and derive statements on the weak convergence of the estimators and use them to develop confidence intervals for new observations. The theory is applied to the special case of high-dimensional time series forecasting. We analyze the behavior of the estimators in simulations based on synthetic data and investigate a real data example with temperature data. The dependency of the data is quantified with absolutely regular beta-mixing coefficients.

Forecasting time series with encoder-decoder neural networks

In this paper, we consider high-dimensional stationary processes where a new observation is generated from a compressed version of past observations. The specific evolution is modeled by an encoder-decoder structure. We estimate the evolution with an encoder-decoder neural network and give upper bounds for the expected forecast error under specific structural and sparsity assumptions. The results are shown separately for conditions either on the absolutely regular mixing coefficients or the functional dependence measure of the observed process. In a quantitative simulation we discuss the behavior of the network estimator under different model assumptions. We corroborate our theory by a real data example where we consider forecasting temperature data.