Items or Relations -- what do Artificial Neural Networks learn?

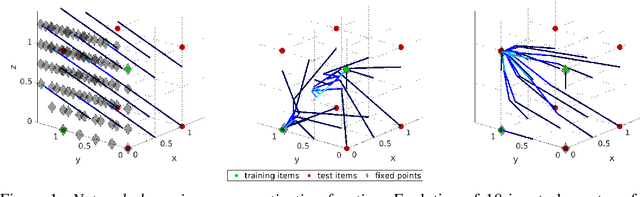
What has an Artificial Neural Network (ANN) learned after being successfully trained to solve a task - the set of training items or the relations between them? This question is difficult to answer for modern applied ANNs because of their enormous size and complexity. Therefore, here we consider a low-dimensional network and a simple task, i.e., the network has to reproduce a set of training items identically. We construct the family of solutions analytically and use standard learning algorithms to obtain numerical solutions. These numerical solutions differ depending on the optimization algorithm and the weight initialization and are shown to be particular members of the family of analytical solutions. In this simple setting, we observe that the general structure of the network weights represents the training set's symmetry group, i.e., the relations between training items. As a consequence, linear networks generalize, i.e., reproduce items that were not part of the training set but are consistent with the symmetry of the training set. In contrast, non-linear networks tend to learn individual training items and show associative memory. At the same time, their ability to generalize is limited. A higher degree of generalization is obtained for networks whose activation function contains a linear regime, such as tanh. Our results suggest ANN's ability to generalize - instead of learning items - could be improved by generating a sufficiently big set of elementary operations to represent relations and strongly depends on the applied non-linearity.

A novel HD Computing Algebra: Non-associative superposition of states creating sparse bundles representing order information

Information inflow into a computational system is by a sequence of information items. Cognitive computing, i.e. performing transformations along that sequence, requires to represent item information as well as sequential information. Among the most elementary operations is bundling, i.e. adding items, leading to 'memory states', i.e. bundles, from which information can be retrieved. If the bundling operation used is associative, e.g. ordinary vector-addition, sequential information can not be represented without imposing additional algebraic structure. A simple stochastic binary bundling rule inspired by the stochastic summation of neuronal activities allows the resulting memory state to represent both, item information as well as sequential information as long as it is non-associative. The memory state resulting from bundling together an arbitrary number of items is non-homogeneous and has a degree of sparseness, which is controlled by the activation threshold in summation. The bundling operation proposed allows to build a filter in the temporal as well as in the items' domain, which can be used to navigate the continuous inflow of information.

Automated fragment identification for electron ionisation mass spectrometry: application to atmospheric measurements of halocarbons

Background: Non-target screening consists in searching a sample for all present substances, suspected or unknown, with very little prior knowledge about the sample. This approach has been introduced more than a decade ago in the field of water analysis, but is still very scarce for indoor and atmospheric trace gas measurements, despite the clear need for a better understanding of the atmospheric trace gas composition. For a systematic detection of emerging trace gases in the atmosphere, a new and powerful analytical method is gas chromatography (GC) of preconcentrated samples, followed by electron ionisation, high resolution mass spectrometry (EI-HRMS). In this work, we present data analysis tools to enable automated identification of unknown compounds measured by GC-EI-HRMS. Results: Based on co-eluting mass/charge fragments, we developed an innovative data analysis method to reliably reconstruct the chemical formulae of the fragments, using efficient combinatorics and graph theory. The method (i) does not to require the presence of the molecular ion, which is absent in $\sim$40% of EI spectra, and (ii) permits to use all measured data while giving more weight to mass/charge ratios measured with better precision. Our method has been trained and validated on >50 halocarbons and hydrocarbons with a molar masses of 30-330 g mol-1 , measured with a mass resolution of approx. 3500. For >90% of the compounds, more than 90% of the reconstructed signal is correct. Cases of wrong identification can be attributed to the scarcity of detected fragments per compound (less than six measured mass/charge) or the lack of isotopic constrain (no rare isotopocule detected). Conclusions: Our method enables to reconstruct most probable chemical formulae independently from spectral databases. Therefore, it demonstrates the suitability of EI-HRMS data for non-target analysis and paves the way for the identification of substances for which no EI mass spectrum is registered in databases. We illustrate the performances of our method for atmospheric trace gases and suggest that it may be well suited for many other types of samples.