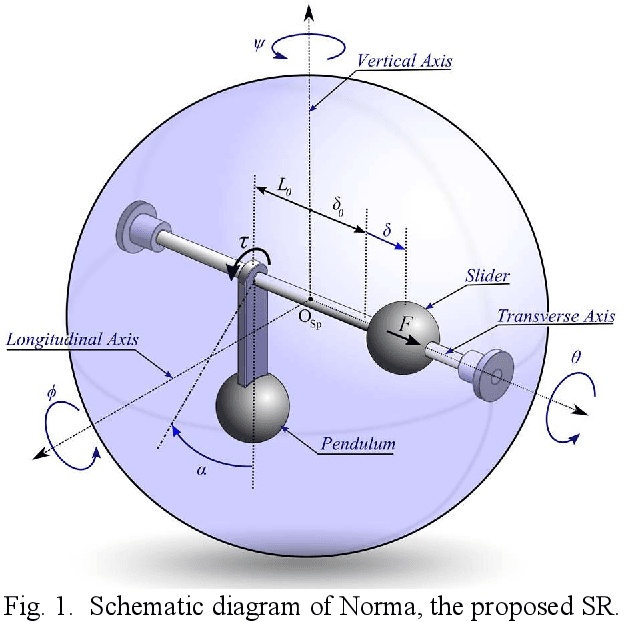
Design, Modeling, and Control of Norma: a Slider & Pendulum-Driven Spherical Robot

This paper discusses the design, modeling, and control of Norma, a novel 2 DOF mobile spherical robot (SR). The propelling mechanism of this robot consists of two actuators: a slider, and a rotational pendulum located on the SR's diagonal shaft. The slider can translate along the shaft and shift the robot's center of gravity towards the robot's sides. The pendulum rotates around the shaft to propel the SR to roll forward and backward. These two actuators enable the SR to perform both rolling and turning maneuvers as a nonholonomic robot. The advantage of the proposed mechanical design lies in its convenience of physical implementation, agility, and accurate mathematical model. The Euler Lagrange approach is utilized to derive the dynamics of the proposed mechanical structure using minimum simplifications possible. Further, a path tracking control scheme is introduced for a smooth trajectory. Finally, simulations are carried out in MATLAB to verify the accuracy of the mathematical model and the effectiveness of the controller against experimental results.

Kinematics of Spherical Robots Rolling Over 3D Terrains

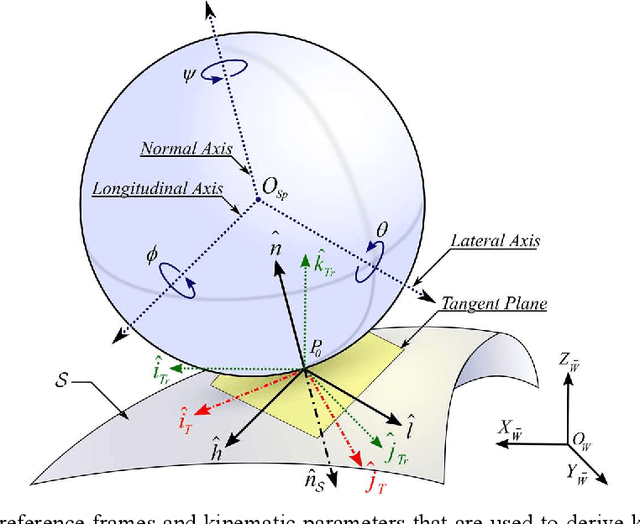
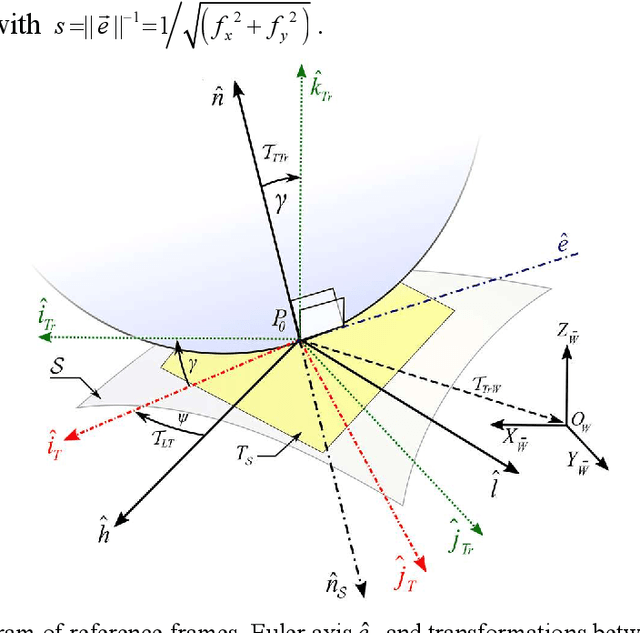
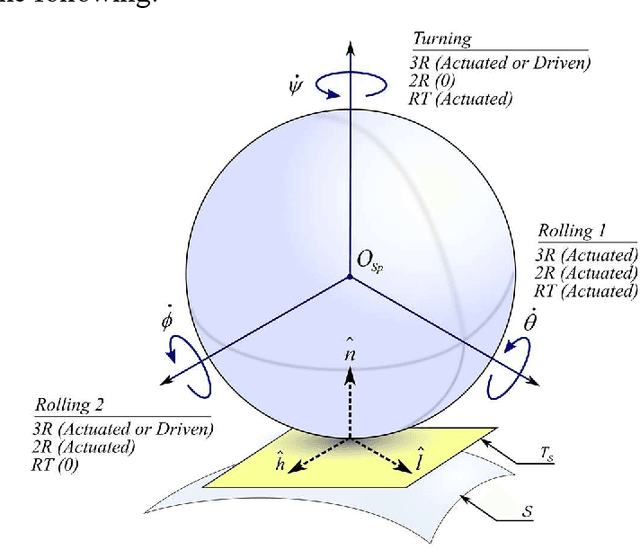
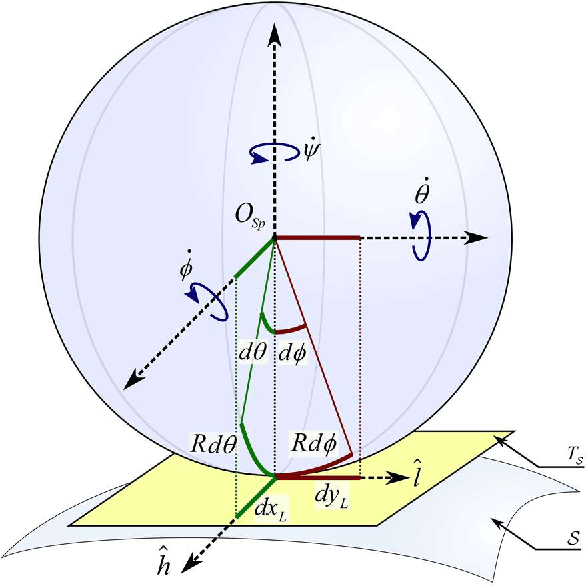
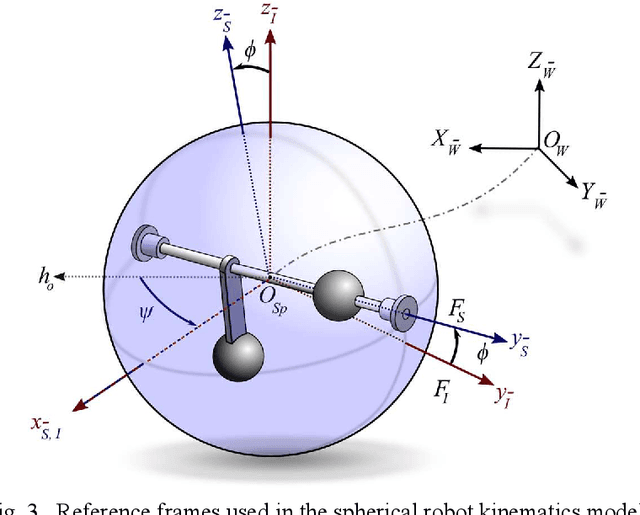
Although the kinematics and dynamics of spherical robots (SRs) on flat horizontal and inclined 2D surfaces are thoroughly investigated, their rolling behavior on generic 3D terrains has remained unexplored. This paper derives the kinematics equations of the most common SRs configurations rolling over 3D surfaces. First, the kinematics equations for a geometrical sphere rolling over a 3D surface are derived along with the characterization of the modeling method. Next, a brief review of current SR mechanical configurations is presented as well as a novel classification for spherical robots based on their kinematics. Then, considering the mechanical constraints of each category, the kinematics equations for each group of spherical robots are presented. Afterwards, a path tracking method is utilized for a desired 3D trajectory. Finally, simulations are carried out to validate the developed models and the effectiveness of the proposed control scheme.