Online Graph Topology Learning from Matrix-valued Time Series

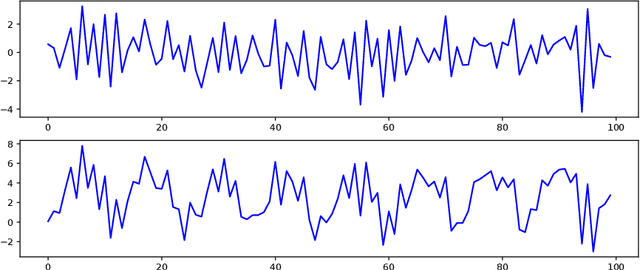
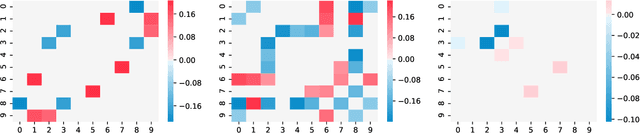
This paper is concerned with the statistical analysis of matrix-valued time series. These are data collected over a network of sensors (typically a set of spatial locations), recording, over time, observations of multiple measurements. From such data, we propose to learn, in an online fashion, a graph that captures two aspects of dependency: one describing the sparse spatial relationship between sensors, and the other characterizing the measurement relationship. To this purpose, we introduce a novel multivariate autoregressive model to infer the graph topology encoded in the coefficient matrix which captures the sparse Granger causality dependency structure present in such matrix-valued time series. We decompose the graph by imposing a Kronecker sum structure on the coefficient matrix. We develop two online approaches to learn the graph in a recursive way. The first one uses Wald test for the projected OLS estimation, where we derive the asymptotic distribution for the estimator. For the second one, we formalize a Lasso-type optimization problem. We rely on homotopy algorithms to derive updating rules for estimating the coefficient matrix. Furthermore, we provide an adaptive tuning procedure for the regularization parameter. Numerical experiments using both synthetic and real data, are performed to support the effectiveness of the proposed learning approaches.

Sensor selection on graphs via data-driven node sub-sampling in network time series

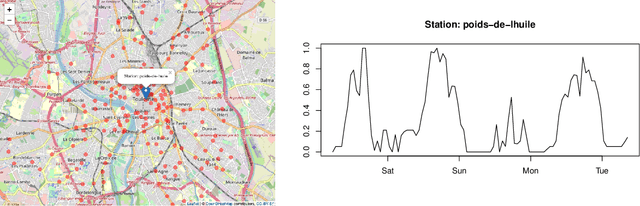
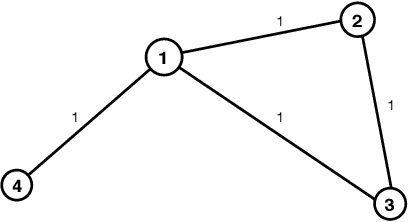
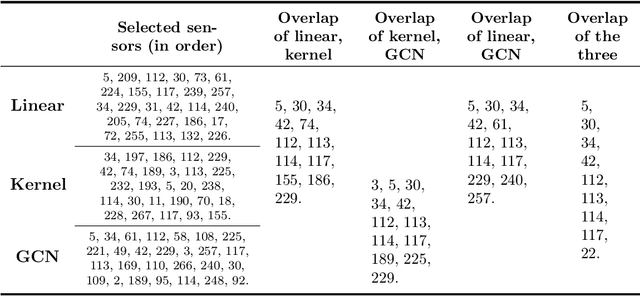
This paper is concerned by the problem of selecting an optimal sampling set of sensors over a network of time series for the purpose of signal recovery at non-observed sensors with a minimal reconstruction error. The problem is motivated by applications where time-dependent graph signals are collected over redundant networks. In this setting, one may wish to only use a subset of sensors to predict data streams over the whole collection of nodes in the underlying graph. A typical application is the possibility to reduce the power consumption in a network of sensors that may have limited battery supplies. We propose and compare various data-driven strategies to turn off a fixed number of sensors or equivalently to select a sampling set of nodes. We also relate our approach to the existing literature on sensor selection from multivariate data with a (possibly) underlying graph structure. Our methodology combines tools from multivariate time series analysis, graph signal processing, statistical learning in high-dimension and deep learning. To illustrate the performances of our approach, we report numerical experiments on the analysis of real data from bike sharing networks in different cities.