Non-Parametric Estimation of Multi-dimensional Marked Hawkes Processes

An extension of the Hawkes process, the Marked Hawkes process distinguishes itself by featuring variable jump size across each event, in contrast to the constant jump size observed in a Hawkes process without marks. While extensive literature has been dedicated to the non-parametric estimation of both the linear and non-linear Hawkes process, there remains a significant gap in the literature regarding the marked Hawkes process. In response to this, we propose a methodology for estimating the conditional intensity of the marked Hawkes process. We introduce two distinct models: \textit{Shallow Neural Hawkes with marks}- for Hawkes processes with excitatory kernels and \textit{Neural Network for Non-Linear Hawkes with Marks}- for non-linear Hawkes processes. Both these approaches take the past arrival times and their corresponding marks as the input to obtain the arrival intensity. This approach is entirely non-parametric, preserving the interpretability associated with the marked Hawkes process. To validate the efficacy of our method, we subject the method to synthetic datasets with known ground truth. Additionally, we apply our method to model cryptocurrency order book data, demonstrating its applicability to real-world scenarios.

A neural network based model for multi-dimensional nonlinear Hawkes processes

This paper introduces the Neural Network for Nonlinear Hawkes processes (NNNH), a non-parametric method based on neural networks to fit nonlinear Hawkes processes. Our method is suitable for analyzing large datasets in which events exhibit both mutually-exciting and inhibitive patterns. The NNNH approach models the individual kernels and the base intensity of the nonlinear Hawkes process using feed forward neural networks and jointly calibrates the parameters of the networks by maximizing the log-likelihood function. We utilize Stochastic Gradient Descent to search for the optimal parameters and propose an unbiased estimator for the gradient, as well as an efficient computation method. We demonstrate the flexibility and accuracy of our method through numerical experiments on both simulated and real-world data, and compare it with state-of-the-art methods. Our results highlight the effectiveness of the NNNH method in accurately capturing the complexities of nonlinear Hawkes processes.

Shallow Neural Hawkes: Non-parametric kernel estimation for Hawkes processes

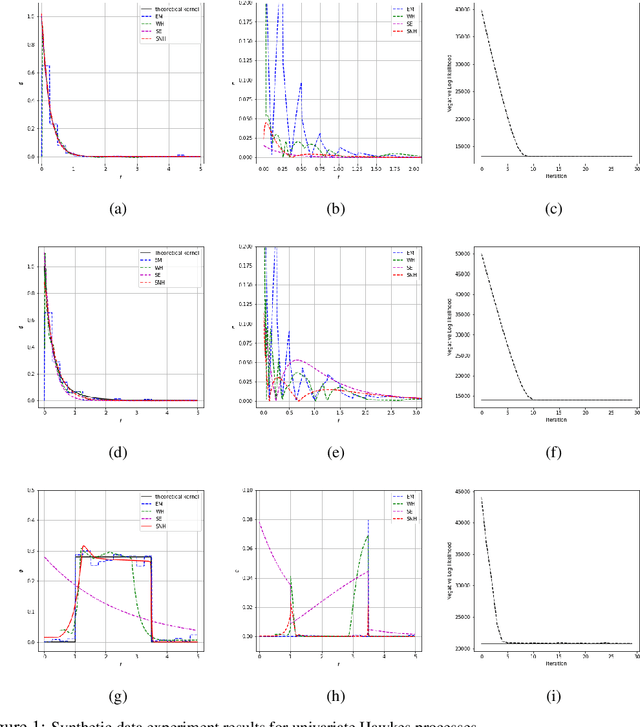
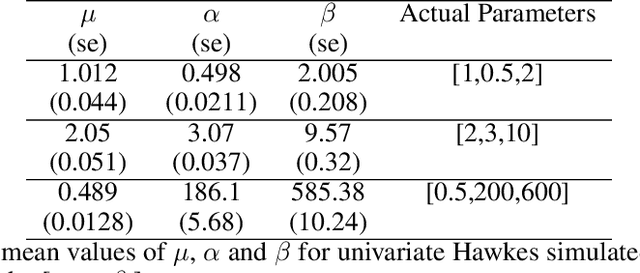
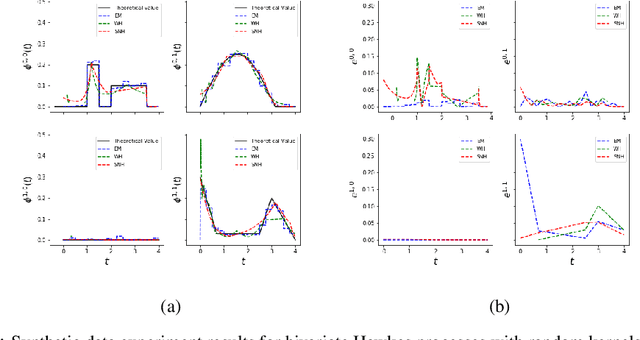
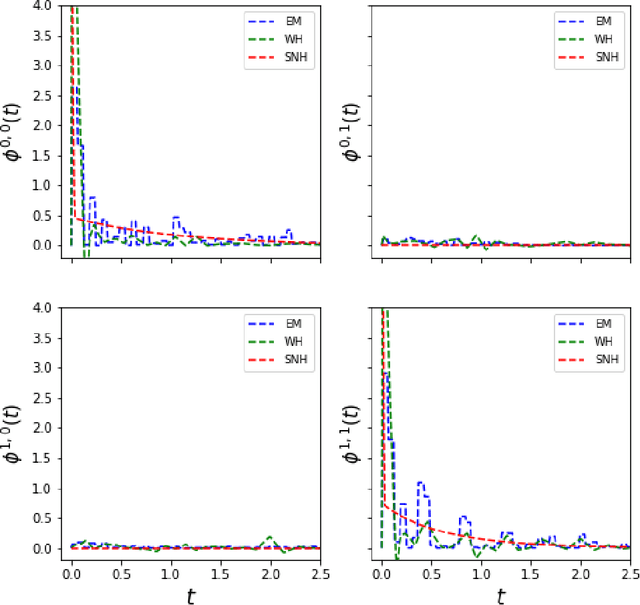
Multi-dimensional Hawkes process (MHP) is a class of self and mutually exciting point processes that find wide range of applications -- from prediction of earthquakes to modelling of order books in high frequency trading. This paper makes two major contributions, we first find an unbiased estimator for the log-likelihood estimator of the Hawkes process to enable efficient use of the stochastic gradient descent method for maximum likelihood estimation. The second contribution is, we propose a specific single hidden layered neural network for the non-parametric estimation of the underlying kernels of the MHP. We evaluate the proposed model on both synthetic and real datasets, and find the method has comparable or better performance than existing estimation methods. The use of shallow neural network ensures that we do not compromise on the interpretability of the Hawkes model, while at the same time have the flexibility to estimate any non-standard Hawkes excitation kernel.