Shallow Neural Hawkes: Non-parametric kernel estimation for Hawkes processes
Paper and Code
Jun 03, 2020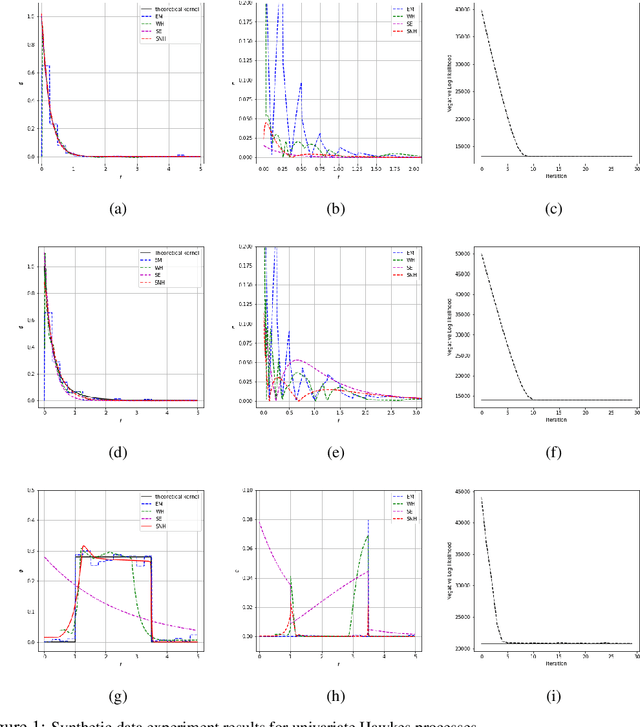
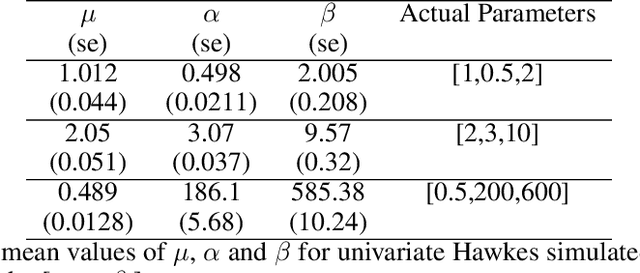
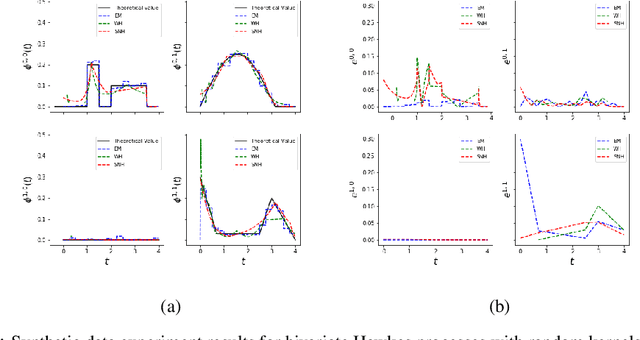
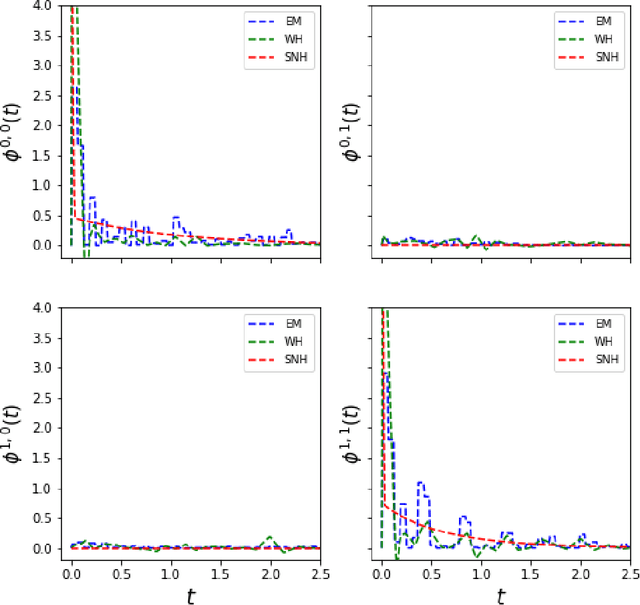
Multi-dimensional Hawkes process (MHP) is a class of self and mutually exciting point processes that find wide range of applications -- from prediction of earthquakes to modelling of order books in high frequency trading. This paper makes two major contributions, we first find an unbiased estimator for the log-likelihood estimator of the Hawkes process to enable efficient use of the stochastic gradient descent method for maximum likelihood estimation. The second contribution is, we propose a specific single hidden layered neural network for the non-parametric estimation of the underlying kernels of the MHP. We evaluate the proposed model on both synthetic and real datasets, and find the method has comparable or better performance than existing estimation methods. The use of shallow neural network ensures that we do not compromise on the interpretability of the Hawkes model, while at the same time have the flexibility to estimate any non-standard Hawkes excitation kernel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge