Sneha Desai
Exploiting Uncertainty of Loss Landscape for Stochastic Optimization
May 30, 2019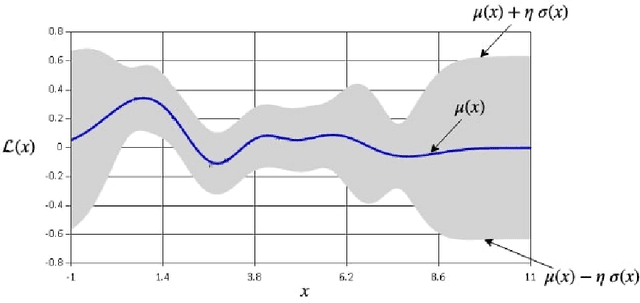
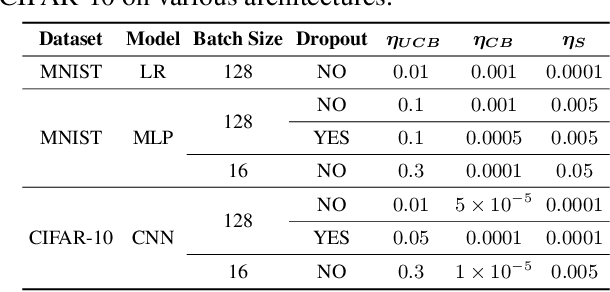

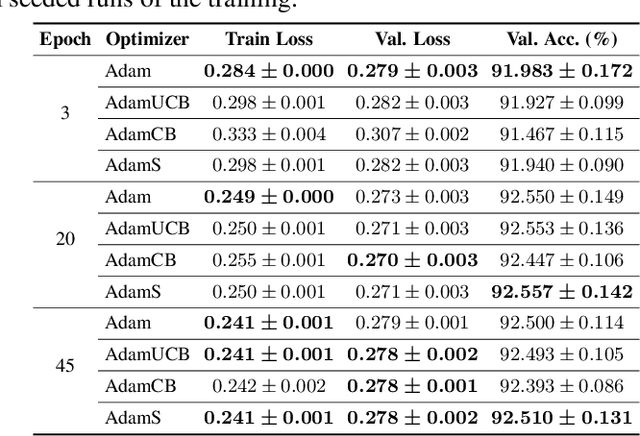
Abstract:We introduce novel variants of momentum by incorporating the variance of the stochastic loss function. The variance characterizes the confidence or uncertainty of the local features of the averaged loss surface across the i.i.d. subsets of the training data defined by the mini-batches. We show two applications of the gradient of the variance of the loss function. First, as a bias to the conventional momentum update to encourage conformity of the local features of the loss function (e.g. local minima) across mini-batches to improve generalization and the cumulative training progress made per epoch. Second, as an alternative direction for "exploration" in the parameter space, especially, for non-convex objectives, that exploits both the optimistic and pessimistic views of the loss function in the face of uncertainty. We also introduce a novel data-driven stochastic regularization technique through the parameter update rule that is model-agnostic and compatible with arbitrary architectures. We further establish connections to probability distributions over loss functions and the REINFORCE policy gradient update with baseline in RL. Finally, we incorporate the new variants of momentum proposed into Adam, and empirically show that our methods improve the rate of convergence of training based on our experiments on the MNIST and CIFAR-10 datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge