Source Enumeration using the Distribution of Angles: A Robust and Parameter-Free Approach

Source enumeration, the task of estimating the number of sources from the signal received by the array of antennas, is a critical problem in array signal processing. Numerous methods have been proposed to estimate the number of sources under white or colored Gaussian noise. However, their performance degrades significantly in the presence of a limited number of observations and/or a large number of sources. In this work, we propose a method based on the distribution of angles that performs well in (a) independent Gaussian, (b) spatially colored Gaussian, and (c) heavy-tailed noise, even when the number of sources is large. We support the supremacy of our algorithm over state-of-the-art methods with extensive simulation results.

Unrolling SVT to obtain computationally efficient SVT for n-qubit quantum state tomography

Quantum state tomography aims to estimate the state of a quantum mechanical system which is described by a trace one, Hermitian positive semidefinite complex matrix, given a set of measurements of the state. Existing works focus on estimating the density matrix that represents the state, using a compressive sensing approach, with only fewer measurements than that required for a tomographically complete set, with the assumption that the true state has a low rank. One very popular method to estimate the state is the use of the Singular Value Thresholding (SVT) algorithm. In this work, we present a machine learning approach to estimate the quantum state of n-qubit systems by unrolling the iterations of SVT which we call Learned Quantum State Tomography (LQST). As merely unrolling SVT may not ensure that the output of the network meets the constraints required for a quantum state, we design and train a custom neural network whose architecture is inspired from the iterations of SVT with additional layers to meet the required constraints. We show that our proposed LQST with very few layers reconstructs the density matrix with much better fidelity than the SVT algorithm which takes many hundreds of iterations to converge. We also demonstrate the reconstruction of the quantum Bell state from an informationally incomplete set of noisy measurements.

Deep learned SVT: Unrolling singular value thresholding to obtain better MSE

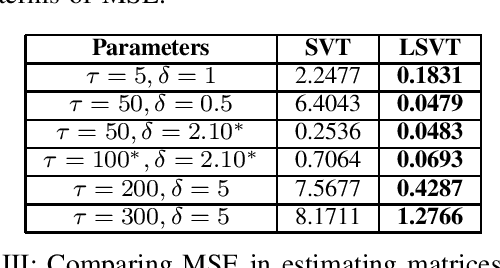
Affine rank minimization problem is the generalized version of low rank matrix completion problem where linear combinations of the entries of a low rank matrix are observed and the matrix is estimated from these measurements. We propose a trainable deep neural network by unrolling a popular iterative algorithm called the singular value thresholding (SVT) algorithm to perform this generalized matrix completion which we call Learned SVT (LSVT). We show that our proposed LSVT with fixed layers (say T) reconstructs the matrix with lesser mean squared error (MSE) compared with that incurred by SVT with fixed (same T) number of iterations and our method is much more robust to the parameters which need to be carefully chosen in SVT algorithm.