Generalized Gaussian Kernel Adaptive Filtering

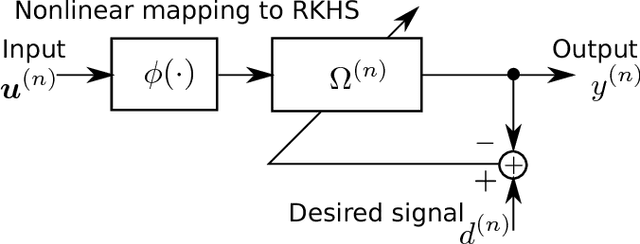
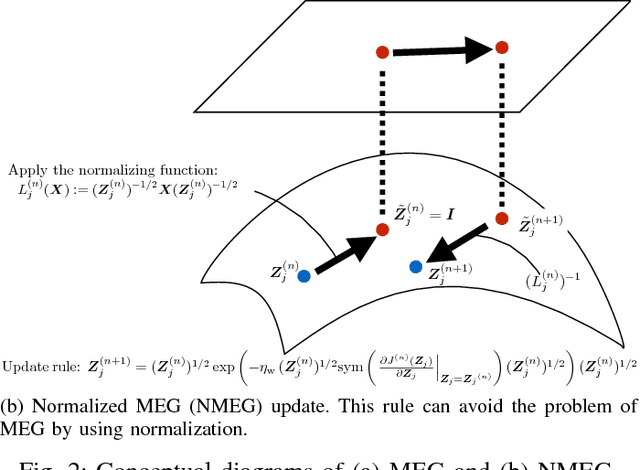
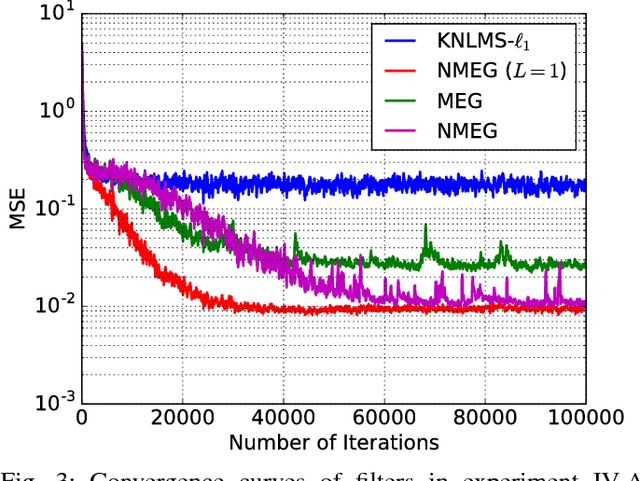
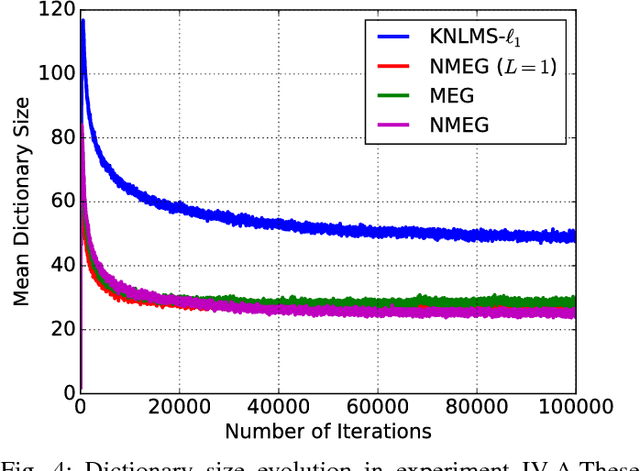
The present paper proposes generalized Gaussian kernel adaptive filtering, where the kernel parameters are adaptive and data-driven. The Gaussian kernel is parametrized by a center vector and a symmetric positive definite (SPD) precision matrix, which is regarded as a generalization of the scalar width parameter. These parameters are adaptively updated on the basis of a proposed least-square-type rule to minimize the estimation error. The main contribution of this paper is to establish update rules for precision matrices on the SPD manifold in order to keep their symmetric positive-definiteness. Different from conventional kernel adaptive filters, the proposed regressor is a superposition of Gaussian kernels with all different parameters, which makes such regressor more flexible. The kernel adaptive filtering algorithm is established together with a l1-regularized least squares to avoid overfitting and the increase of dimensionality of the dictionary. Experimental results confirm the validity of the proposed method.

Visualization of Manifold-Valued Elements by Multidimensional Scaling

The present contribution suggests the use of a multidimensional scaling (MDS) algorithm as a visualization tool for manifold-valued elements. A visualization tool of this kind is useful in signal processing and machine learning whenever learning/adaptation algorithms insist on high-dimensional parameter manifolds.