Simon Pfingstl
On Integrating Prior Knowledge into Gaussian Processes for Prognostic Health Monitoring
Jun 17, 2022
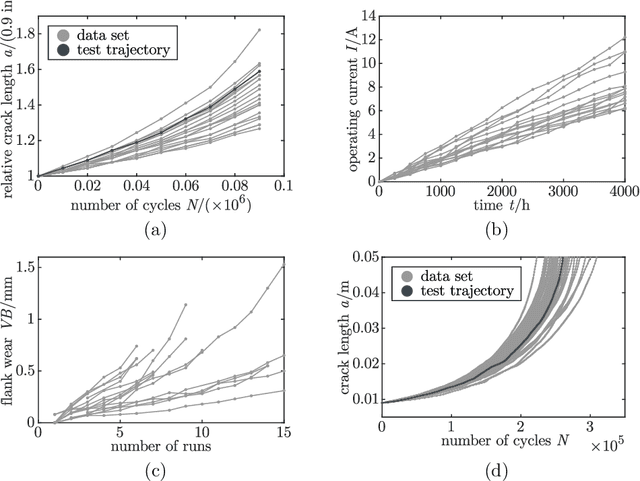

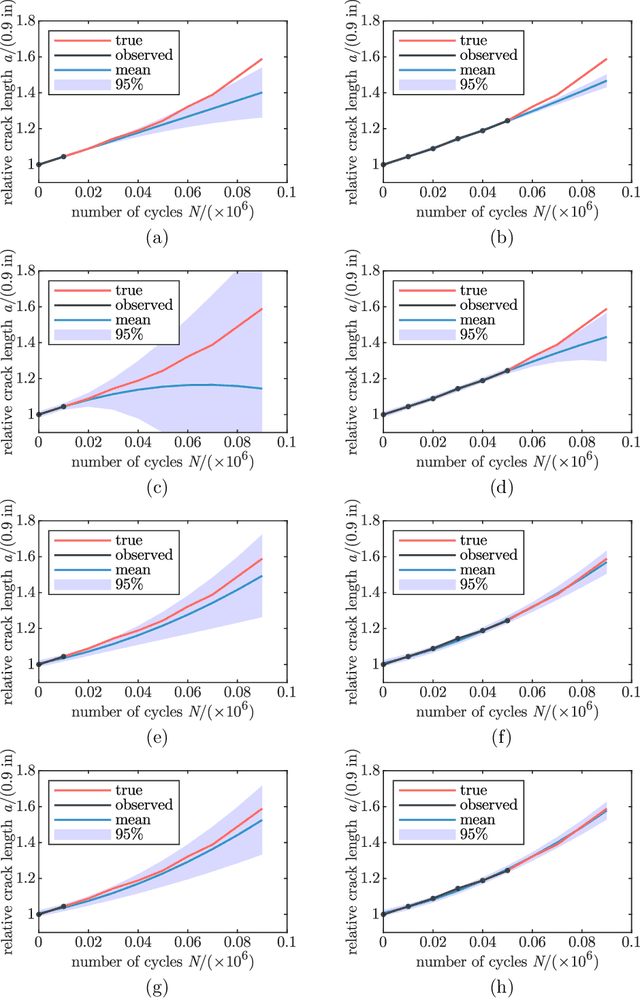
Abstract:Gaussian process regression is a powerful method for predicting states based on given data. It has been successfully applied for probabilistic predictions of structural systems to quantify, for example, the crack growth in mechanical structures. Typically, predefined mean and covariance functions are employed to construct the Gaussian process model. Then, the model is updated using current data during operation while prior information based on previous data is ignored. However, predefined mean and covariance functions without prior information reduce the potential of Gaussian processes. This paper proposes a method to improve the predictive capabilities of Gaussian processes. We integrate prior knowledge by deriving the mean and covariance functions from previous data. More specifically, we first approximate previous data by a weighted sum of basis functions and then derive the mean and covariance functions directly from the estimated weight coefficients. Basis functions may be either estimated or derived from problem-specific governing equations to incorporate physical information. The applicability and effectiveness of this approach are demonstrated for fatigue crack growth, laser degradation, and milling machine wear data. We show that well-chosen mean and covariance functions, like those based on previous data, significantly increase look-ahead time and accuracy. Using physical basis functions further improves accuracy. In addition, computation effort for training is significantly reduced.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge