Superposition for Lambda-Free Higher-Order Logic

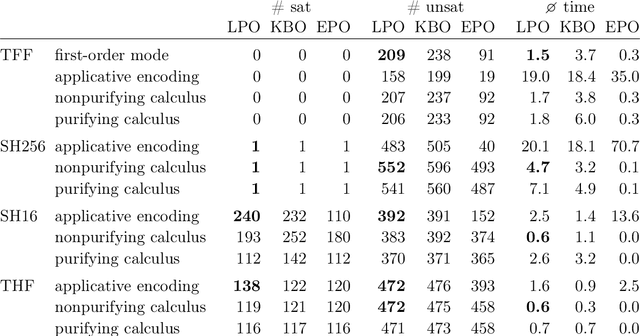
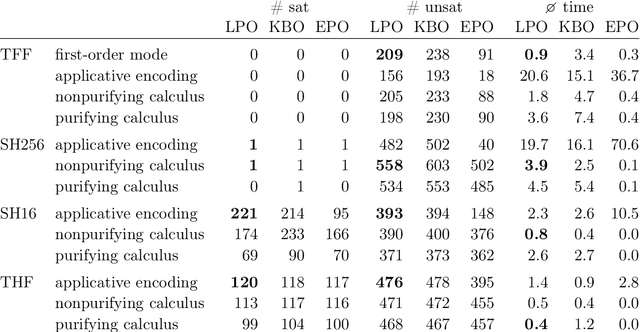
We introduce refutationally complete superposition calculi for intentional and extensional clausal $\lambda$-free higher-order logic, two formalisms that allow partial application and applied variables. The calculi are parameterized by a term order that need not be fully monotonic, making it possible to employ the $\lambda$-free higher-order lexicographic path and Knuth-Bendix orders. We implemented the calculi in the Zipperposition prover and evaluated them on Isabelle/HOL and TPTP benchmarks. They appear promising as a stepping stone towards complete, highly efficient automatic theorem provers for full higher-order logic.

The Imandra Automated Reasoning System (system description)

We describe Imandra, a modern computational logic theorem prover designed to bridge the gap between decision procedures such as SMT, semi-automatic inductive provers of the Boyer-Moore family like ACL2, and interactive proof assistants for typed higher-order logics. Imandra's logic is computational, based on a pure subset of OCaml in which all functions are terminating, with restrictions on types and higher-order functions that allow conjectures to be translated into multi-sorted first-order logic with theories, including arithmetic and datatypes. Imandra has novel features supporting large-scale industrial applications, including a seamless integration of bounded and unbounded verification, first-class computable counterexamples, efficiently executable models and a cloud-native architecture supporting live multiuser collaboration. The core reasoning mechanisms of Imandra are (i) a semi-complete procedure for finding models of formulas in the logic mentioned above, centered around the lazy expansion of recursive functions, and (ii) an inductive waterfall and simplifier which "lifts" many Boyer-Moore ideas to our typed higher-order setting. These mechanisms are tightly integrated and subject to many forms of user control. Imandra's user interfaces include an interactive toplevel, Jupyter notebooks and asynchronous document-based verification (in the spirit of Isabelle's Prover IDE) with VS Code.