Stochastic Subgraph Neighborhood Pooling for Subgraph Classification

Subgraph classification is an emerging field in graph representation learning where the task is to classify a group of nodes (i.e., a subgraph) within a graph. Subgraph classification has applications such as predicting the cellular function of a group of proteins or identifying rare diseases given a collection of phenotypes. Graph neural networks (GNNs) are the de facto solution for node, link, and graph-level tasks but fail to perform well on subgraph classification tasks. Even GNNs tailored for graph classification are not directly transferable to subgraph classification as they ignore the external topology of the subgraph, thus failing to capture how the subgraph is located within the larger graph. The current state-of-the-art models for subgraph classification address this shortcoming through either labeling tricks or multiple message-passing channels, both of which impose a computation burden and are not scalable to large graphs. To address the scalability issue while maintaining generalization, we propose Stochastic Subgraph Neighborhood Pooling (SSNP), which jointly aggregates the subgraph and its neighborhood (i.e., external topology) information without any computationally expensive operations such as labeling tricks. To improve scalability and generalization further, we also propose a simple data augmentation pre-processing step for SSNP that creates multiple sparse views of the subgraph neighborhood. We show that our model is more expressive than GNNs without labeling tricks. Our extensive experiments demonstrate that our models outperform current state-of-the-art methods (with a margin of up to 2%) while being up to 3X faster in training.

Simplifying Subgraph Representation Learning for Scalable Link Prediction

Link prediction on graphs is a fundamental problem in graph representation learning. Subgraph representation learning approaches (SGRLs), by transforming link prediction to graph classification on the subgraphs around the target links, have advanced the learning capability of Graph Neural Networks (GNNs) for link prediction. Despite their state-of-the-art performance, SGRLs are computationally expensive, and not scalable to large-scale graphs due to their expensive subgraph-level operations for each target link. To unlock the scalability of SGRLs, we propose a new class of SGRLs, that we call Scalable Simplified SGRL (S3GRL). Aimed at faster training and inference, S3GRL simplifies the message passing and aggregation operations in each link's subgraph. S3GRL, as a scalability framework, flexibly accommodates various subgraph sampling strategies and diffusion operators to emulate computationally-expensive SGRLs. We further propose and empirically study multiple instances of S3GRL. Our extensive experiments demonstrate that the proposed S3GRL models scale up SGRLs without any significant performance compromise (even with considerable gains in some cases), while offering substantially lower computational footprints (e.g., multi-fold inference and training speedup).

Sampling Enclosing Subgraphs for Link Prediction

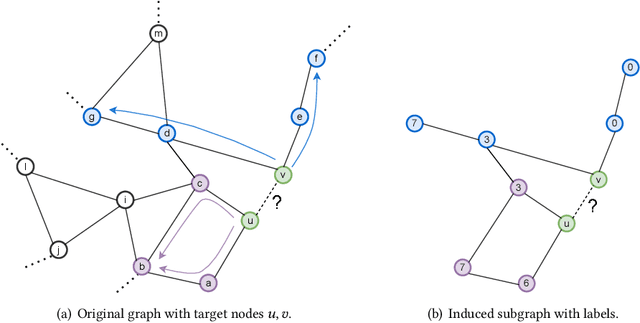
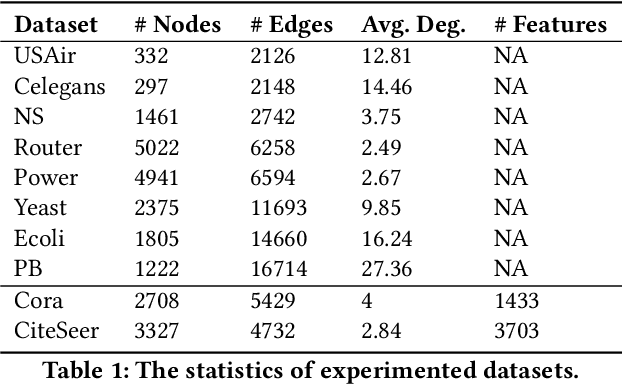
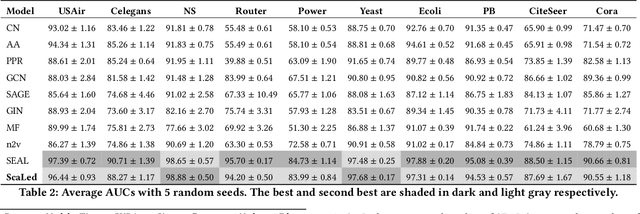
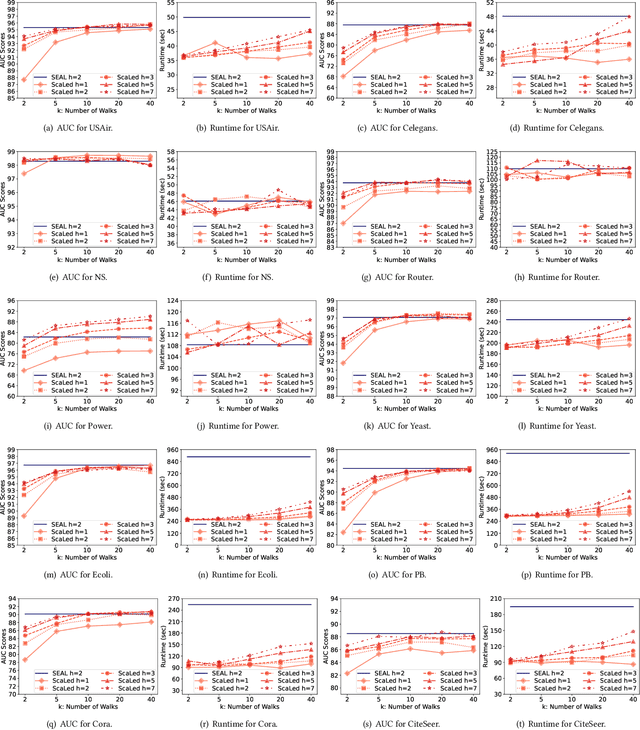
Link prediction is a fundamental problem for graph-structured data (e.g., social networks, drug side-effect networks, etc.). Graph neural networks have offered robust solutions for this problem, specifically by learning the representation of the subgraph enclosing the target link (i.e., pair of nodes). However, these solutions do not scale well to large graphs as extraction and operation on enclosing subgraphs are computationally expensive, especially for large graphs. This paper presents a scalable link prediction solution, that we call ScaLed, which utilizes sparse enclosing subgraphs to make predictions. To extract sparse enclosing subgraphs, ScaLed takes multiple random walks from a target pair of nodes, then operates on the sampled enclosing subgraph induced by all visited nodes. By leveraging the smaller sampled enclosing subgraph, ScaLed can scale to larger graphs with much less overhead while maintaining high accuracy. ScaLed further provides the flexibility to control the trade-off between computation overhead and accuracy. Through comprehensive experiments, we have shown that ScaLed can produce comparable accuracy to those reported by the existing subgraph representation learning frameworks while being less computationally demanding.