Efficient Graph Matching for Correlated Stochastic Block Models

We study learning problems on correlated stochastic block models with two balanced communities. Our main result gives the first efficient algorithm for graph matching in this setting. In the most interesting regime where the average degree is logarithmic in the number of vertices, this algorithm correctly matches all but a vanishing fraction of vertices with high probability, whenever the edge correlation parameter $s$ satisfies $s^2 > \alpha \approx 0.338$, where $\alpha$ is Otter's tree-counting constant. Moreover, we extend this to an efficient algorithm for exact graph matching whenever this is information-theoretically possible, positively resolving an open problem of R\'acz and Sridhar (NeurIPS 2021). Our algorithm generalizes the recent breakthrough work of Mao, Wu, Xu, and Yu (STOC 2023), which is based on centered subgraph counts of a large family of trees termed chandeliers. A major technical challenge that we overcome is dealing with the additional estimation errors that are necessarily present due to the fact that, in relevant parameter regimes, the latent community partition cannot be exactly recovered from a single graph. As an application of our results, we give an efficient algorithm for exact community recovery using multiple correlated graphs in parameter regimes where it is information-theoretically impossible to do so using just a single graph.

One-shot Neural Backdoor Erasing via Adversarial Weight Masking

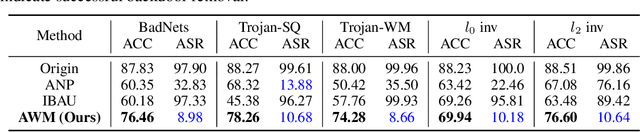
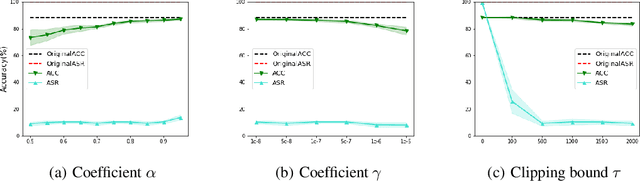
Recent studies show that despite achieving high accuracy on a number of real-world applications, deep neural networks (DNNs) can be backdoored: by injecting triggered data samples into the training dataset, the adversary can mislead the trained model into classifying any test data to the target class as long as the trigger pattern is presented. To nullify such backdoor threats, various methods have been proposed. Particularly, a line of research aims to purify the potentially compromised model. However, one major limitation of this line of work is the requirement to access sufficient original training data: the purifying performance is a lot worse when the available training data is limited. In this work, we propose Adversarial Weight Masking (AWM), a novel method capable of erasing the neural backdoors even in the one-shot setting. The key idea behind our method is to formulate this into a min-max optimization problem: first, adversarially recover the trigger patterns and then (soft) mask the network weights that are sensitive to the recovered patterns. Comprehensive evaluations of several benchmark datasets suggest that AWM can largely improve the purifying effects over other state-of-the-art methods on various available training dataset sizes.