Shuizheng Zhou
Stable Sparse Subspace Embedding for Dimensionality Reduction
Feb 07, 2020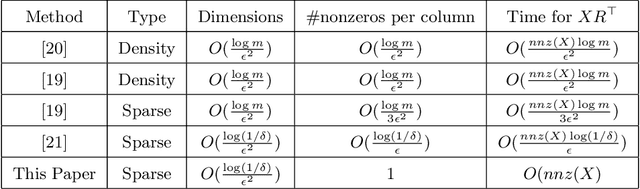


Abstract:Sparse random projection (RP) is a popular tool for dimensionality reduction that shows promising performance with low computational complexity. However, in the existing sparse RP matrices, the positions of non-zero entries are usually randomly selected. Although they adopt uniform sampling with replacement, due to large sampling variance, the number of non-zeros is uneven among rows of the projection matrix which is generated in one trial, and more data information may be lost after dimension reduction. To break this bottleneck, based on random sampling without replacement in statistics, this paper builds a stable sparse subspace embedded matrix (S-SSE), in which non-zeros are uniformly distributed. It is proved that the S-SSE is stabler than the existing matrix, and it can maintain Euclidean distance between points well after dimension reduction. Our empirical studies corroborate our theoretical findings and demonstrate that our approach can indeed achieve satisfactory performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge