Fighting Sample Degeneracy and Impoverishment in Particle Filters: A Review of Intelligent Approaches

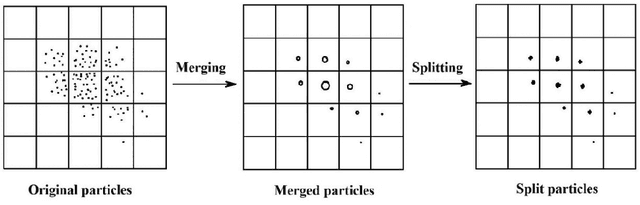
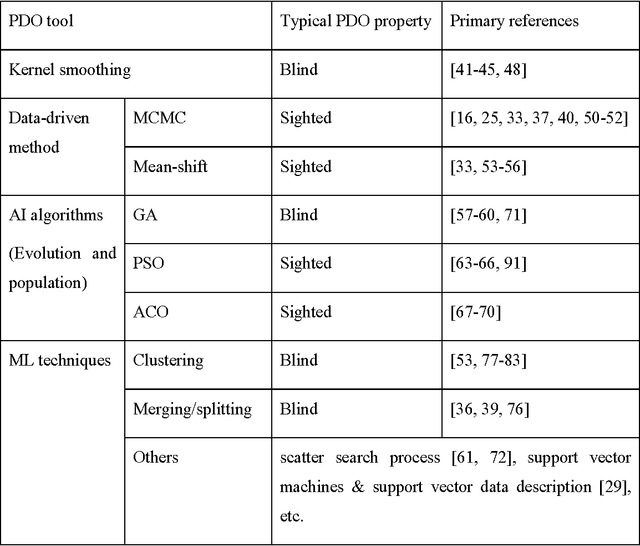
During the last two decades there has been a growing interest in Particle Filtering (PF). However, PF suffers from two long-standing problems that are referred to as sample degeneracy and impoverishment. We are investigating methods that are particularly efficient at Particle Distribution Optimization (PDO) to fight sample degeneracy and impoverishment, with an emphasis on intelligence choices. These methods benefit from such methods as Markov Chain Monte Carlo methods, Mean-shift algorithms, artificial intelligence algorithms (e.g., Particle Swarm Optimization, Genetic Algorithm and Ant Colony Optimization), machine learning approaches (e.g., clustering, splitting and merging) and their hybrids, forming a coherent standpoint to enhance the particle filter. The working mechanism, interrelationship, pros and cons of these approaches are provided. In addition, Approaches that are effective for dealing with high-dimensionality are reviewed. While improving the filter performance in terms of accuracy, robustness and convergence, it is noted that advanced techniques employed in PF often causes additional computational requirement that will in turn sacrifice improvement obtained in real life filtering. This fact, hidden in pure simulations, deserves the attention of the users and designers of new filters.

Adapting sample size in particle filters through KLD-resampling

This letter provides an adaptive resampling method. It determines the number of particles to resample so that the Kullback-Leibler distance (KLD) between distribution of particles before resampling and after resampling does not exceed a pre-specified error bound. The basis of the method is the same as Fox's KLD-sampling but implemented differently. The KLD-sampling assumes that samples are coming from the true posterior distribution and ignores any mismatch between the true and the proposal distribution. In contrast, we incorporate the KLD measure into the resampling in which the distribution of interest is just the posterior distribution. That is to say, for sample size adjustment, it is more theoretically rigorous and practically flexible to measure the fit of the distribution represented by weighted particles based on KLD during resampling than in sampling. Simulations of target tracking demonstrate the efficiency of our method.