Robust Learning for Optimal Dynamic Treatment Regimes with Observational Data

Many public policies and medical interventions involve dynamics in their treatment assignments, where treatments are sequentially assigned to the same individuals across multiple stages, and the effect of treatment at each stage is usually heterogeneous with respect to the history of prior treatments and associated characteristics. We study statistical learning of optimal dynamic treatment regimes (DTRs) that guide the optimal treatment assignment for each individual at each stage based on the individual's history. We propose a step-wise doubly-robust approach to learn the optimal DTR using observational data under the assumption of sequential ignorability. The approach solves the sequential treatment assignment problem through backward induction, where, at each step, we combine estimators of propensity scores and action-value functions (Q-functions) to construct augmented inverse probability weighting estimators of values of policies for each stage. The approach consistently estimates the optimal DTR if either a propensity score or Q-function for each stage is consistently estimated. Furthermore, the resulting DTR can achieve the optimal convergence rate $n^{-1/2}$ of regret under mild conditions on the convergence rate for estimators of the nuisance parameters.

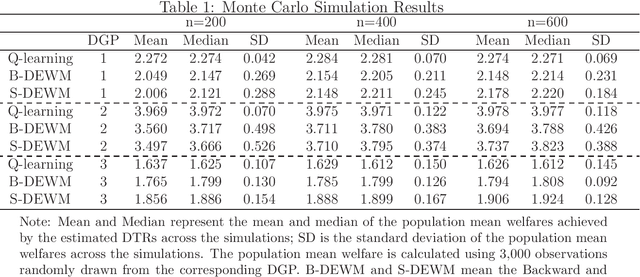
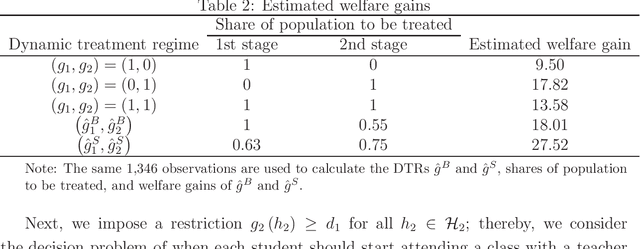
Estimation of Optimal Dynamic Treatment Assignment Rules under Policy Constraint

This paper studies statistical decisions for dynamic treatment assignment problems. Many policies involve dynamics in their treatment assignments where treatments are sequentially assigned to individuals across multiple stages and the effect of treatment at each stage is usually heterogeneous with respect to the prior treatments, past outcomes, and observed covariates. We consider estimating an optimal dynamic treatment rule that guides the optimal treatment assignment for each individual at each stage based on the individual's history. This paper proposes an empirical welfare maximization approach in a dynamic framework. The approach estimates the optimal dynamic treatment rule from panel data taken from an experimental or quasi-experimental study. The paper proposes two estimation methods: one solves the treatment assignment problem at each stage through backward induction, and the other solves the whole dynamic treatment assignment problem simultaneously across all stages. We derive finite-sample upper bounds on the worst-case average welfare-regrets for the proposed methods and show $n^{-1/2}$-minimax convergence rates. We also modify the simultaneous estimation method to incorporate intertemporal budget/capacity constraints.

Constrained Classification and Policy Learning

Modern machine learning approaches to classification, including AdaBoost, support vector machines, and deep neural networks, utilize surrogate loss techniques to circumvent the computational complexity of minimizing empirical classification risk. These techniques are also useful for causal policy learning problems, since estimation of individualized treatment rules can be cast as a weighted (cost-sensitive) classification problem. Consistency of the surrogate loss approaches studied in Zhang (2004) and Bartlett et al. (2006) crucially relies on the assumption of correct specification, meaning that the specified set of classifiers is rich enough to contain a first-best classifier. This assumption is, however, less credible when the set of classifiers is constrained by interpretability or fairness, leaving the applicability of surrogate loss based algorithms unknown in such second-best scenarios. This paper studies consistency of surrogate loss procedures under a constrained set of classifiers without assuming correct specification. We show that in the setting where the constraint restricts the classifier's prediction set only, hinge losses (i.e., $\ell_1$-support vector machines) are the only surrogate losses that preserve consistency in second-best scenarios. If the constraint additionally restricts the functional form of the classifier, consistency of a surrogate loss approach is not guaranteed even with hinge loss. We therefore characterize conditions for the constrained set of classifiers that can guarantee consistency of hinge risk minimizing classifiers. Exploiting our theoretical results, we develop robust and computationally attractive hinge loss based procedures for a monotone classification problem.