Estimation of Optimal Dynamic Treatment Assignment Rules under Policy Constraint
Paper and Code
Jul 07, 2021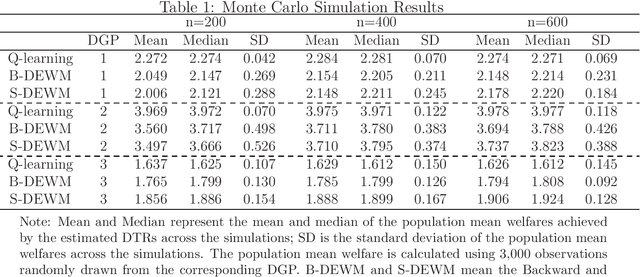
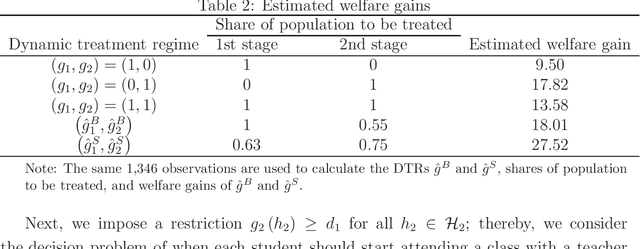

This paper studies statistical decisions for dynamic treatment assignment problems. Many policies involve dynamics in their treatment assignments where treatments are sequentially assigned to individuals across multiple stages and the effect of treatment at each stage is usually heterogeneous with respect to the prior treatments, past outcomes, and observed covariates. We consider estimating an optimal dynamic treatment rule that guides the optimal treatment assignment for each individual at each stage based on the individual's history. This paper proposes an empirical welfare maximization approach in a dynamic framework. The approach estimates the optimal dynamic treatment rule from panel data taken from an experimental or quasi-experimental study. The paper proposes two estimation methods: one solves the treatment assignment problem at each stage through backward induction, and the other solves the whole dynamic treatment assignment problem simultaneously across all stages. We derive finite-sample upper bounds on the worst-case average welfare-regrets for the proposed methods and show $n^{-1/2}$-minimax convergence rates. We also modify the simultaneous estimation method to incorporate intertemporal budget/capacity constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge