Concentration of the exponential mechanism and differentially private multivariate medians

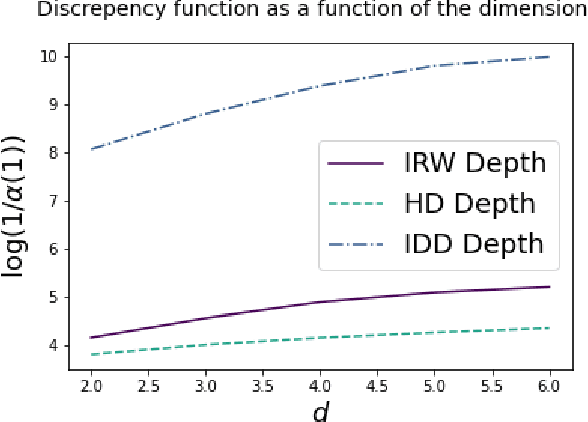
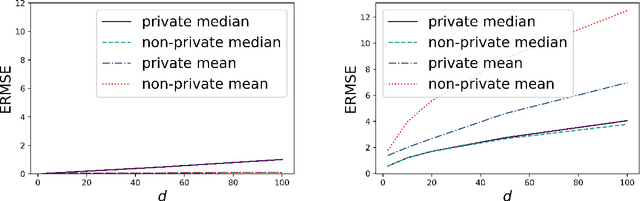
We prove concentration inequalities for the output of the exponential mechanism about the maximizer of the population objective function. This bound applies to objective functions that satisfy a mild regularity condition. To illustrate our result, we study the problem of differentially private multivariate median estimation. We present novel finite-sample performance guarantees for differentially private multivariate depth-based medians which are essentially sharp. Our results cover commonly used depth functions, such as the halfspace (or Tukey) depth, spatial depth, and the integrated dual depth. We show that under Cauchy marginals, the cost of heavy-tailed location estimation outweighs the cost of privacy. We demonstrate our results numerically using a Gaussian contamination model in dimensions up to $d = 100$, and compare them to a state-of-the-art private mean estimation algorithm.