Designing faster mixed integer linear programming algorithm via learning the optimal path

Designing faster algorithms for solving Mixed-Integer Linear Programming (MILP) problems is highly desired across numerous practical domains, as a vast array of complex real-world challenges can be effectively modeled as MILP formulations. Solving these problems typically employs the branch-and-bound algorithm, the core of which can be conceived as searching for a path of nodes (or sub-problems) that contains the optimal solution to the original MILP problem. Traditional approaches to finding this path rely heavily on hand-crafted, intuition-based heuristic strategies, which often suffer from unstable and unpredictable performance across different MILP problem instances. To address this limitation, we introduce DeepBound, a deep learning-based node selection algorithm that automates the learning of such human intuition from data. The core of DeepBound lies in learning to prioritize nodes containing the optimal solution, thereby improving solving efficiency. DeepBound introduces a multi-level feature fusion network to capture the node representations. To tackle the inherent node imbalance in branch-and-bound trees, DeepBound employs a pairwise training paradigm that enhances the model's ability to discriminate between nodes. Extensive experiments on three NP-hard MILP benchmarks demonstrate that DeepBound achieves superior solving efficiency over conventional heuristic rules and existing learning-based approaches, obtaining optimal feasible solutions with significantly reduced computation time. Moreover, DeepBound demonstrates strong generalization capability on large and complex instances. The analysis of its learned features reveals that the method can automatically discover more flexible and robust feature selection, which may effectively improve and potentially replace human-designed heuristic rules.

NIERT: Accurate Numerical Interpolation through Unifying Scattered Data Representations using Transformer Encoder

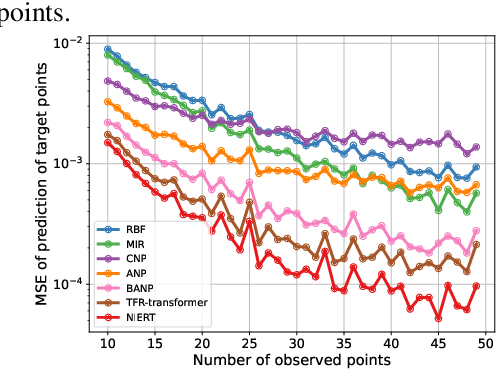
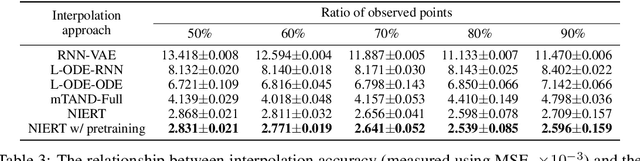
Numerical interpolation for scattered data, i.e., estimating values for target points based on those of some observed points, is widely used in computational science and engineering. The existing approaches either require explicitly pre-defined basis functions, which makes them inflexible and limits their performance in practical scenarios, or train neural networks as interpolators, which still have limited interpolation accuracy as they treat observed and target points separately and cannot effectively exploit the correlations among data points. Here, we present a learning-based approach to numerical interpolation for scattered data using encoder representation of Transformers (called NIERT). Unlike the recent learning-based approaches, NIERT treats observed and target points in a unified fashion through embedding them into the same representation space, thus gaining the advantage of effectively exploiting the correlations among them. The specially-designed partial self-attention mechanism used by NIERT makes it escape from the unexpected interference of target points on observed points. We further show that the partial self-attention is essentially a learnable interpolation module combining multiple neural basis functions, which provides interpretability of NIERT. Through pre-training on large-scale synthetic datasets, NIERT achieves considerable improvement in interpolation accuracy for practical tasks. On both synthetic and real-world datasets, NIERT outperforms the existing approaches, e.g., on the TFRD-ADlet dataset for temperature field reconstruction, NIERT achieves an MAE of $1.897\times 10^{-3}$, substantially better than the state-of-the-art approach (MAE: $27.074\times 10^{-3}$). The source code of NIERT is available at https://anonymous.4open.science/r/NIERT-2BCF.